Algebraic reasoning
Term 2 starting in week 5 :: Estimated time: 2 weeks
- Simplify complex expressions
- Find the rule for the nth term of a linear sequence (review)
- Use rules for sequences
- Solve linear simultaneous equations (review)
For higher-attaining pupils:
- Solve simultaneous equations with one quadratic (review)
- Find the rule for the nth term of a quadratic sequence (review)
- Formal algebraic proof Inequalities in two variables
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Steps Investigate the numbers associated with this growing sequence of steps made from Multilink cubes.
Mix and Math Determine the nature of adding, subtracting and multiplying numbers with specific properties.
Missing Terms Can you work out which numbers are missing from these number sequences?
Leapfrog An investigation of the minimum number of moves required to make the blue and green frogs swap places.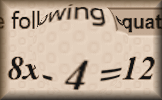
Words and Concepts Fill in the missing words to show an understanding of the vocabulary of equations, inequalities, angles and shapes.
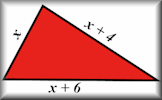Algebraic Perimeters Questions about the perimeters and areas of polygons given as algebraic expressions.
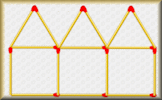Matchstick Patterns Create a formula to describe the nth term of a sequence by examining the structure of the diagrams.
Simultaneous Shopping Find the cost of the individual items in shopping baskets (introduction to simultaneous equations).
Sequence Generator An online app which produces number sequences as words.
Watsadoo Rotate the cogs to catch the flying numbers in the correct sections.
Algebra In Action Real life problems adapted from an old Mathematics textbook which can be solved using algebra.
Superfluous Find a strategy to figure out the values of the letters used in these calculations.
Octagon Loops Investigate the features of loops created from octagons.
Arithmetic Sequences An exercise on linear sequences including finding an expression for the nth term and the sum of n terms.
Identity, Equation or Formula? Arrange the given statements in groups to show whether they are identities, equations or formulae.
Trapezia Which numbers can be represented by groups of circles arranged in the shape of a trapezium?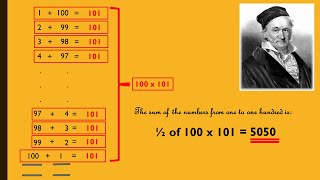
Arithmetic Sequences Video A reminder of how to find the next term, the nth term and the sum of terms of an arithmetic or linear sequence.
Prison Cell Problem A number patterns investigation involving prisoners and prison guards.
Inequalities Check that you know what inequality signs mean and how they are used to compare two quantities. Includes negative numbers, decimals, fractions and metric measures.
Geometric Sequences An exercise on geometric sequences including finding the nth term and the sum of any number of terms.
Quick Add 'Em Quiz Find the sum of a sequence of consecutive numbers using a quick, efficient, elegant method.
Geometric Sequences Video Revise all you need to know about geometric sequences and series.
Linear Programming A selection of linear programming questions with an interactive graph plotting tool.
True or False? Arrange the given statements in groups to show whether they are always true, sometimes true or false.
Simultaneous Equations Video Learn to solve simultaneous equations from the very basic to those containing quadratics. This video is to help you do the online, self-marking exercise.
Simultaneous Equations A self-marking, multi-level set of exercises on solving pairs of simultaneous equations.
Aunt Lucy's Legacy Decide which of the four schemes Aunt Lucy proposes will provide the most money. This investigation involves the sum of sequences as well as considering life expectancy.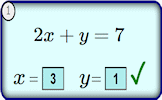
Diophantine Equations Practise finding integer solutions to equations with more than one unknown.
Fibonacci Quest A number of self marking quizzes based on the fascinating Fibonacci Sequence.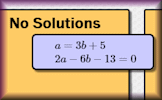
Simultaneous Solutions Arrange the given pairs of simultaneous equations in groups to show whether they have no solution, one solution or infinite solutions.
Handshakes If everyone in this room shook hands with each other, how many handshakes would there be?
Unbeknownst Some picture grid puzzles which can be solved by using simultaneous equations.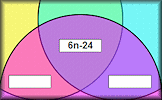
Venn Diagram of Sequences Find the formula for the nth term of sequences that belong in the given sets.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.
Algebraic Proof A video explaining how to approach algebraic proof. This is suitable for students on a higher GCSE course.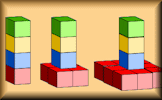
Quadratic and Cubic Sequences Deduce expressions to calculate the nth term of quadratic and cubic sequences.
Sequences Table Challenge Complete the table showing the terms of the sequences and the formulas for the nth terms.
Parts of Sequences Find the formula that describes the part of the sequence that can be seen
Here are some exam-style questions on this topic:
- "The first five terms of an arithmetic sequence are:" ... more
- "The diagram shows an isosceles triangle (not drawn to scale)." ... more
- "Nora and Dora are trying to solve the following simultaneous equations by finding the intersection of their graphs." ... more
- "The diagrams show a triangle and a rectangle (not drawn to scale)." ... more
- "The perimeter of the triangle is the same length as the perimeter of the square." ... more
- "The red line in the diagram below shows an inequality. If the variable is \(x\), which inequality best describes \(x\)?" ... more
- "(a) Write down the integer values of \(x\) that satisfy the inequality \(–3 \le x \lt 1 \)." ... more
- "(a) Solve 9m < 15m − 12" ... more
- "The graph of a quadratic function, \(y=f(x)\) is shown drawn accurately in the following diagram. Write down all the integer solutions of \(f(x) \le 0\)." ... more
- "Aimee, Natasha and Ruby play hockey." ... more
- "Here is a picture of four models. Some of the cubes are hidden behind other cubes." ... more
- "The diagram below is a sketch of \(y = f(x)\) where \(f(x)\) is a quadratic function." ... more
- "(a) On the grid, draw the lines of \(y = x + 5 \) and \(x + y = 4\)." ... more
- "In a sequence" ... more
- "Describe the unshaded (white) region by writing down three inequalities." ... more
- "(a) Use the red graphs to solve the simultaneous equations:" ... more
- "Luke, Leia and Han swim lengths of a swimming pool to raise money for charity." ... more
- "(a) Find the \(n\)th term of the sequence 7, 13, 19, 25,..." ... more
- "The straight line \(y = 3x - 4\) intersects the curve \(y = x^2 + 4x – 7\) at the points \(A\) and \(B\)." ... more
- "On the grid below indicate the region that satisfies all three of these inequalities." ... more
- "(a) The expression \( (x+1)(2x-3)(3x+4) \) can be written in the form \(ax^3 + bx^2 + cx + d \) where \(a, b, c\) and \(d\) are integers. Find the values of \(a, b, c\) and \(d\)." ... more
- "Solve the simultaneous equations" ... more
- "Two rectangles, not drawn to scale, are shown below. All measurements are in centimetres. Both rectangles have the same areas. Work out the perimeter of the rectangle on the left." ... more
- "A region on a coordinate grid is described by the following three inequalities:" ... more
- "By shading the unwanted regions, show the region satisfied by these three inequalities." ... more
- "Solve the following inequalities then explain how the whole number solutions to A and B are different." ... more
- "Estimate the solutions of the following simultaneous equations using their graphs as drawn on the grid below." ... more
- "Solve the simultaneous equations:" ... more
- "The area of rectangle PQRS (not to scale) is 80cm2. " ... more
- "A large car park has an area of 1400m2 with space for \(x\) cars and \(y\) vans. Each car requires 14m2 of space and each van requires 35m2 of space." ... more
- "A rectangular sheet of paper can be cut into two identical rectangular pieces in two different ways, either by cutting along line A or by cutting along line B." ... more
- "A region on a coordinate grid is described by the following three inequalities:" ... more
- "Show that you understand equations and inequalities by answering the following:" ... more
- "State whether each of the following statements is true or false. Give reasons for your answers." ... more
- "One is added to the product of two consecutive positive even numbers. Show that the result is a square number." ... more
- "Draw the graph of \(y = 2x^2 + 3x - 7\) for \( -3.5 \le x \le 2\). Draw suitable straight lines to find approximate solutions (to one decimal place) of the equations:" ... more
- "A large mug of hot tea is cooling on a small lounge table." ... more
- "Rätselzeit school has an annual sports day in which the mathematics teachers are in charge of the scoring system." ... more
- "(a) Give a reason why 0 is an even number." ... more
- "Betsy thinks that \((3x)^2\) is always greater than or equal to \(3x\)." ... more
- "This expression can be used to generate a sequence of numbers." ... more
- "Here is a function machine that produces two outputs, A and B." ... more
- "Work out an expression for the nth term of the quadratic sequence" ... more
- "Given that \(n\) can be any integer such that \(n \gt 1\), prove that \(n^2 + 3n\) is even." ... more
- "Solve \(2x^2 + 7x - 15 <0\)" ... more
- "Here are the first six terms of a quadratic sequence." ... more
- "Solve algebraically the simultaneous equations to find the solution where \(-10 \le x \le 10\)." ... more
- "Find an expression, in terms of \(n\), for the \(n\)th term of the sequence that has the following first five terms:" ... more
- "Two numbers are chosen so that the sum of their squares is 25." ... more
- "m and n are positive whole numbers with m > n" ... more
- "Here are the first six terms of a quadratic sequence." ... more
- "The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre." ... more
- "The diagrams below show a sequence of patterns made from red and yellow tiles." ... more
- "(a) A sequence is defined by the following rule where \(u_n\) is the \(n^{th}\) term of the sequence:" ... more
- "Express as a single fraction and simplify your answer." ... more
- "The prices of two watches are in the ratio \(a:b\)." ... more
- "(a) Prove that the product of two consecutive whole numbers is always even." ... more
- "The number \(T\) can be expressed as \(T = 4k + 3\) where \(k\) is a positive integer." ... more
- "Prove that the expression below is always positive." ... more
- "The first three and last terms of an arithmetic sequence are \(7,13,19,...,1357\)" ... more
- "An arithmetic sequence is given by 6, 13, 20, …" ... more
- "In an arithmetic sequence, the fifth term is 44 and the ninth term is 80." ... more
- "A square is drawn with sides of length 32 cm. The midpoints of the sides of this square are joined to form a new square and four red triangles. The process is repeated to produce yellow triangles and then again to produce blue triangles." ... more
- "A celebrity football match is planned to take place in a large stadium." ... more
- "The first term of an infinite geometric sequence is 10. The sum of the infinite sequence is 500." ... more
- "A Grecian amphitheatre was built in the form of a horseshoe and has 22 rows." ... more
- "In a geometric series the common ratio is \(r\) and sum to \(n\) terms is \(S_n\)." ... more
- "Chris checks his Twitter account and notices that he received a tweet at 8:00am. At 8:05am he forwards the tweet to four people. Five minutes later, those four people each forward the tweet to four new people. Assume this pattern continues and each time the tweet is sent to people who have not received it before." ... more
- "The sum of the first n terms of a geometric sequence is given by:" ... more
- "Consider the sum of the squares of any two consecutive odd integers." ... more
Here are some Advanced Starters on this statement:
- Car Inequalities
Solve three simultaneous inequalities to find how many cars I own. more - Exceeds by 99
Find the number whose double exceeds its half by exactly 99. more - Grandmother
How far would grandma have travelled after a suitably large number of days given her walking regime? more - Piece of String
Find where a piece of string should be cut to form a circle and a square of equal areas. more - Reverse Connection
Find a general rule for the difference between a two digit number and that same number with the digits reversed. more - Same Series Sum
Find an arithmetic series and a geometric series that have the same sum of the first five terms. more - Two Equals One
What is wrong with the algebraic reasoning that shows that 2 = 1 ? more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
- Number Spotting patterns is an important skill in many areas of life. The world of numbers contains many fascinating patterns and understanding them enables better problem solving strategies. From seeing patterns in the multiples of numbers shaded in a hundred square to spotting the recurring sequences of digits in decimal numbers there is a great deal for pupils to be introduced to. This topic includes even, odd, prime, triangular, perfect, abundant, square and cube numbers. It uses factors and multiples to find solutions to real life problems and encourages number connections to be investigated for pleasure. There are a lot of puzzles, challenges and games too. See also the Mental Methods topic and our Number Skills Inventory.
- Sequences A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them. The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms. Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom. Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.
- Simultaneous Equations This topic covers simultaneous equations with two different variables. The starters pose real world problems which can be solved using the techniques taught at school or by other intuitive methods. Though there are many formal strategies for solving simultaneous equations the skill of forming the equations from real life situations is a very important stage in working towards a solution. Algebraic methods are the most efficient for solving basic simultaneous equations but graphical methods, probably using a graphic display calculator or computer software package, may be more suitable for less standard sets of simultaneous equations.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Name Again
Work out what the nth letter will be in a recurring pattern of letters in a person's name
2nd Lesson
Missing Terms
Find the missing terms from these linear sequences.
3rd Lesson
One one
Continue the given number pattern with the help of a little lateral thinking.
4th Lesson
True or False?
An activity designed to address common misconceptions.
5th Lesson
Sequence Dancing
Find the next term of the number sequences.
6th Lesson
Windmill Sequence
Find the value of the missing term of the sequence. It is easier than you may think!
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
