Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Welcome to the Transum Newsletter for October 2024, and, as you'd expect, I can't resist the temptation to begin with a Halloween-themed puzzle.
Vesper bought a number of pumpkins in one shop at the rate of 4 for £20.
He then buys the same number of pumpkins in another shop at a rate of 6 for £20.
What was the mean number of pumpkins that could be bought for £20?

If you get an answer I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email: gro.musnarT@rettelsweN. The solution and the credit for this puzzle will be in next month's Newsletter.
While you think about that here are some of the key resources added to the Transum website during the last month.
Diophantine Equations is a new set of exercises providing students with a quest to find whole numbers that make the equations true. The equations have more than one unknown so traditional equation solving techniques won't work. Try it yourself if you haven't encountered Diophantine equations before.
Framed Numbers is a new Starter but is also included on the Maths Puzzles page. I've adapted this challenge from one I've seen in a number of places but as yet I haven't found the original source of the idea. It surprisingly lends itself to a trial-and-improvement strategy though it's quite different from other maths puzzles.
Platonic Solids is new and will hopefully help pupils understand basic geometric concepts such as faces, edges, and vertices. Level 2 brings in the nets of the solids which will add to the range of nets exercises on Transum.
It really makes my day when I receive information about someone who has spent quality time using a Transum resource. This particular instance gave me a jaw-dropping moment: a video of Gracie Schwartz completing Level 1 of 'Divides Exactly' in just six seconds.
Video of Gracie's record breaking performance
I love the cries of "Got it, I got it, I got it" at the end. Now there's a challenge for your students!
On the 3rd of October there's an excuse to be poetic. It's World Poetry Day and, yes, you guessed it, I have created a page of mathematical poems for you to enjoy. I have predictably called this resource Maths Poems and the page contains links to topic specific poems I have written and collected over the years.
The month of October ends with Halloween. The Starter of the Day for the 31st has spooky music and screams, making the day memorable while solving ghostly maths problems. [See also: Trick or Treat, Squorder and Double, Double, Halve and Treble.]
There’s only one thing I don’t like about Halloween… which is …
My friend Allan, who teaches at an international school in Germany using a German-language textbook, sometimes shares interesting snippets from their curriculum. One such topic, not typically covered in the British curriculum, is Heron's method (Der Heron-Algorithmus). This ancient algorithm, devised by Heron of Alexandria in first-century Egypt, was the earliest known way to compute square roots. The method involves making an initial guess and repeatedly refining it by averaging the guess with the quotient of the number divided by that guess. Though not widely taught today, Heron's method remains a brilliant example of early algorithmic thinking. You can try it using these Square Roots.

A new area on the Transum website has been set up to celebrate the History of Mathematics. I do not need tell you more about this resource thanks to my next discovery (in the next paragraph)
As you know I have been fascinated by the recent avalanche of new Artificial Intelligence facilities. My latest discovery is NotebookLM. The Audio Overview feature in Google NotebookLM is designed to transform uploaded documents into engaging audio discussions. This feature aims to help users understand complex information by generating a conversational summary presented by two AI hosts. So I gave it the new History of Mathematics resource and it came up with a 13 minute discussion. You can hear it in the Transum Podcast which is the audio version of this newsletter. To say I was incredibly impressed is the understatement of the year.
Finally the answer to last month's puzzle which was:
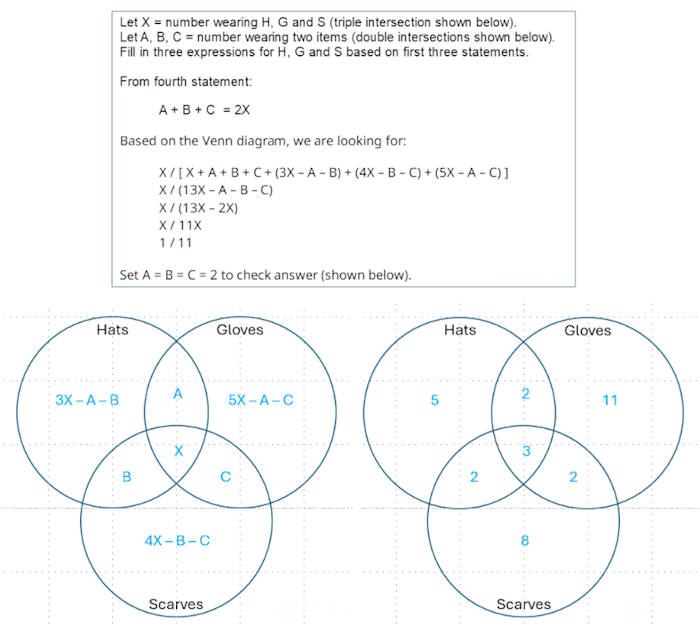
In preparation for the cold weather, a large group of people dressed warmly in different ways.
What fraction of the group wore all three items: hats, scarves and gloves?
The answer is one eleventh.
The first five puzzle solutions were received from Kevin, Mala, Rick, Leonard and Shreyak.
Thanks to everyone who sent in their thoughts. You can see some working below.
That's all for now,
John
PS. I couldn't decide whether to teach my students the sine rule this Halloween or just hand out some Cadbury Mini Chocolates.
So, I asked them: "Trig or Treat?"
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Kevin, Yeppoon
Sunday, September 1, 2024
" "
"
Rick, US
Tuesday, September 3, 2024
"Initially, I tried solving using variables, but as a blind person, this became too difficult to manage in my head. Since only a fraction was required, I arbitrarily chose a number for the people wearing all three items and proceeded from there. I also assumed there were no people waring none of the items, since this would make it impossible to determine a fraction.
Assume there are 100 people who wear all three items. Then, there are 400 people wearing hats, 500 people wearing scarfs, and 600 people wearing gloves. We also know that there are 200 people wearing only two items. The rest must be waring only one item. Since we do not care which two items are being worn, let’s assume that 200 people wearing hats also wore scarfs. That leaves 100 people wearing only hats, 200 people wearing only scarfs, and 500 people wearing only gloves. Adding these all together: 100 all three, 200 only two, 100 hats, 200 scarfs, and 500 gloves equals 1100 people in total. Therefore, one in 11, or approximately 9%, of the total group wore all three items. "
Leonard, US
Saturday, September 7, 2024
" "
"