Types of number and sequences
Term 3 starting in week 9 :: Estimated time: 2 weeks
- Understand the difference between factors and multiples (review)
- Understand primes and express a number as a product of its prime factors (review)
- Find the HCF and LCM of a set of numbers (review)
- Describe and continue arithmetic and geometric sequences
- Explore other sequences
- Find the rule for the nth term of a linear sequence (review)
For higher-attaining pupils:
- Describe and continue sequences involving surds
- Find the rule for the nth term of a quadratic sequence
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Prime Pips in Pots This is a version of Wari, one of the oldest known games to still be widely played today. It involves small prime numbers.
Number Grids Investigate the properties of number with these interactive number grids.
Prime Numbers Video A reminder of what prime numbers and composite numbers are.
Prime Numbers Jigsaw Interactive jigsaw puzzles of different types of grids containing prime numbers.
Steps Investigate the numbers associated with this growing sequence of steps made from Multilink cubes.
Finding Prime Factors A straight forward explanation from SLEP
Prime Path Pace The objective is to find a continuous path of prime numbers in the shortest time.
Factor Trees Create factor trees to find the prime factors of the given numbers.
Flabbergasted Game This game for one or two players is an exciting challenge to demonstrate an understanding of factors and multiples.
Least Common Multiple A cartoon from Smile and Learn with very easy examples of how to find the LCM of two numbers.
Product of Primes Match the primes that multiply to give the products. A drag and drop activity.
Prime Labyrinth Find the path to the centre of the labyrinth by moving along the prime numbers.
Convoluted Find the runs of four multiples in order as quickly as you can.
Connect 4 Factors This a game for one or two players. The winner is the first to line up four numbers with a common factor.
Fractionagons Calculate the missing fractions in these partly completed arithmagon puzzles.
Missing Terms Can you work out which numbers are missing from these number sequences?
Pick The Primes Pick the prime fruit from the tree as quickly as possible. Practise to improve your personal best time.
HCF and LCM Video Learn different methods for finding the highest common factor and lowest common multiple of two or three numbers.
HCF and LCM Practise finding the highest common factor (H.C.F), sometimes called the greatest common divisor, and the lowest common multiple (L.C.M) of two numbers.
Leapfrog An investigation of the minimum number of moves required to make the blue and green frogs swap places.
HCF and LCM Calculator A demonstration of how to find the highest common factor (HCF or GCD) and the lowest common multiple (LCM) of two numbers.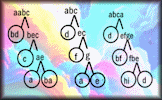
Factor Trees Challenge Can you determine the unique digits that will complete these factor trees?
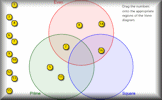Venn Diagram Place each of the numbers 1 to 16 on the correct regions on the Venn diagram.
Dump-A-Dice Race An online board game for two players involving prime and square numbers and making choices.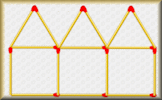
Matchstick Patterns Create a formula to describe the nth term of a sequence by examining the structure of the diagrams.
Sequence Generator An online app which produces number sequences as words.
Watsadoo Rotate the cogs to catch the flying numbers in the correct sections.
Number Skills Inventory A checklist of basic numeracy techniques that every pupil should know.
Divisibility Test Practise using the quick ways to spot whether a number is divisible by the digits two to nine.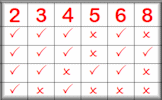
Divisibility Tests 2-12 A visual aid designed to be projected in the classroom. Here you can find the quick ways of telling whether a number is exactly divisible by the numbers two to twelve.
Prime Pairs Game A game for two players who take turns to select two numbers that add up to a prime number.
Goal Products Arrange the numbered footballs on the goal posts to make three, 3-number products that are all the same.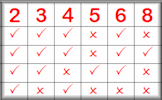
Divisibility Tests Worksheet This worksheet contains a list of the divisibility tests along with a fill-in-the-table exercise.
In Terms of Pi Circle related questions requiring the answer to include a multiple of pi rather than an approximation.
Scallywags and Scoundrels Arrange the scallywags and scoundrels on the chairs so that the numbers of any two sitting next to each other add up to a prime number.
Three Prime Sum A self-marking challenge to write each of the given numbers as the sum of three prime numbers.
Arithmetic Sequences An exercise on linear sequences including finding an expression for the nth term and the sum of n terms.
Trapezia Which numbers can be represented by groups of circles arranged in the shape of a trapezium?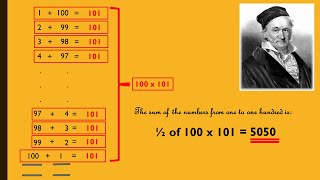
Arithmetic Sequences Video A reminder of how to find the next term, the nth term and the sum of terms of an arithmetic or linear sequence.
Prison Cell Problem A number patterns investigation involving prisoners and prison guards.
Geometric Sequences An exercise on geometric sequences including finding the nth term and the sum of any number of terms.
Product Square Arrange the given numbers in a three by three grid to obtain the diagonal, row and column products.
Geometric Sequences Video Revise all you need to know about geometric sequences and series.
What Are They? An online exercise about sums, products, differences, ratios, square and prime numbers.
Satisfy Place the nine numbers in the table so they obey the row and column headings about the properties of the numbers.
Aunt Lucy's Legacy Decide which of the four schemes Aunt Lucy proposes will provide the most money. This investigation involves the sum of sequences as well as considering life expectancy.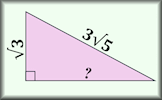
Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.
Three Ways Find three different ways of multiplying four different digits together to get the given target number. There are nine levels for this online challenge.
Snooker Investigation Investigate a special snooker table with only four pockets. Which pocket will the ball fall into for various sized snooker tables?
Prime Square Drag the numbers into the red cells so that the sum of the three numbers in each row and each column is a prime number.
Fibonacci Quest A number of self marking quizzes based on the fascinating Fibonacci Sequence.
Handshakes If everyone in this room shook hands with each other, how many handshakes would there be?
Doughnut Dissection A puzzle to find four different ways of making 900 by multiplying together three different numbers.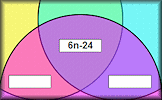
Venn Diagram of Sequences Find the formula for the nth term of sequences that belong in the given sets.
Delightfully Divisible Arrange the digits one to nine to make a number which is divisible in the way described.
Surds Learn that a surd is an irrational number and how to simplify expressions including surds. This video is to help you do the online exercise.
Sieve of Eratosthenes A self checking, interactive version of the Sieve of Eratosthenes method of finding prime numbers.
Square and Cube Roots Find square roots and cube roots by first calculating the prime factorisation of a number.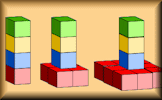
Quadratic and Cubic Sequences Deduce expressions to calculate the nth term of quadratic and cubic sequences.
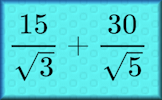Surds A self-marking exercise on calculating, simplifying and manipulating surds (also known as radicals).
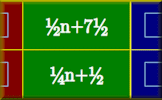Sequences Table Challenge Complete the table showing the terms of the sequences and the formulas for the nth terms.
Parts of Sequences Find the formula that describes the part of the sequence that can be seen
Some Sums and Products Number puzzles involving adding, multiplying and problem solving
Here are some exam-style questions on this topic:
- "(a) Write 90 as a product of its prime factors." ... more
- "The first five terms of an arithmetic sequence are:" ... more
- "Find the highest common factor (HCF) of 60 and 96." ... more
- "Without using a calculator:" ... more
- "Write 250 as a product of powers of its prime factors." ... more
- "Show that 206 can be written as the sum of a power of five and a square number." ... more
- "Here is a picture of four models. Some of the cubes are hidden behind other cubes." ... more
- "In a sequence" ... more
- "The number, \(N\), can be written as the product of prime factors in index form as:" ... more
- "(a) Find the \(n\)th term of the sequence 7, 13, 19, 25,..." ... more
- "A circular dart board has radius of 30 cm." ... more
- "A large mug of hot tea is cooling on a small lounge table." ... more
- "Here is a list of five numbers." ... more
- "This expression can be used to generate a sequence of numbers." ... more
- "Work out an expression for the nth term of the quadratic sequence" ... more
- "(a) Express \( \sqrt{5} + \sqrt{20} \) in the form \( a \sqrt{5} \) where \(a\) is an integer." ... more
- "Here are the first six terms of a quadratic sequence." ... more
- "Find an expression, in terms of \(n\), for the \(n\)th term of the sequence that has the following first five terms:" ... more
- "Here are the first six terms of a quadratic sequence." ... more
- "The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre." ... more
- "The diagrams below show a sequence of patterns made from red and yellow tiles." ... more
- "(a) A sequence is defined by the following rule where \(u_n\) is the \(n^{th}\) term of the sequence:" ... more
- "(a) Write this list of numbers in order, smallest first." ... more
- "A celebrity football match is planned to take place in a large stadium." ... more
- "The cosine of acute angle \( \alpha \) is \( \frac{1}{ \sqrt 5} \)" ... more
Here are some Advanced Starters on this statement:
- HCF and LCM given
If given the HCF, LCM can you find the numbers? more - Same Series Sum
Find an arithmetic series and a geometric series that have the same sum of the first five terms. more - Seventeen Camels
Explain the mathematics of the classic ninteenth century fraction sharing story. more - Single Fraction
Simplify an expression involving fractions, exponents and a square root. more - Test Scores
Explore the misconception that when adding fractions you add both the numerators and the denominators more - Weather Reports
Which five different integers multiply together to give 12? more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Factors A factor is a whole number that divides exactly into another whole number. We say the first number is a factor of the second number. Prime numbers only have two factors, one and themselves. After becoming familiar with times tables pupils then practise using this knowledge by recognising factors of numbers. There are well known and some less well known divisibility tests that are of some use in solving more complex number problems. Pupils need to know how to find the highest common factor (HCF) of two or more numbers either mentally or using a pen and paper strategy so that they can correctly manipulate fractions and algebraic expressions.
- LCM LCM stands for lowest common multiple or least common multiple. The LCM of two (or more numbers) is the smallest number that both of the numbers divide into exactly. Being able to find the LCM is useful when trying to find a common denominator when adding two fractions together. The LCM also describes the points when two (or more) periodic repetitions coincide. HCF stands for highest common factor which is also known as the greatest common factor. The HCF of two (or more) numbers is the largest number that divides into the two numbers exactly. Being able to find the HCF is useful in everyday organisational tasks and also when factorising algebraic expressions.
- Number Spotting patterns is an important skill in many areas of life. The world of numbers contains many fascinating patterns and understanding them enables better problem solving strategies. From seeing patterns in the multiples of numbers shaded in a hundred square to spotting the recurring sequences of digits in decimal numbers there is a great deal for pupils to be introduced to. This topic includes even, odd, prime, triangular, perfect, abundant, square and cube numbers. It uses factors and multiples to find solutions to real life problems and encourages number connections to be investigated for pleasure. There are a lot of puzzles, challenges and games too. See also the Mental Methods topic and our Number Skills Inventory.
- Roots Pupils should learn how to find real roots associated with integer powers (square root, cube root and higher). They should also learn to distinguish between exact representations of roots and their decimal approximations. Just how do you find the cube root of a number? By trial and improvement, iterative calculations or by learning to use a calculator efficiently?
- Sequences A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them. The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms. Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom. Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Sign Sequences
Continue the sequences if you can work out the rule.
2nd Lesson
To Be Continued
Work out the next term in the given sequences.
3rd Lesson
Vixen Value
The Vixen Value of a word is the number of vowels multiplied by the number of consonants. How many words can you find with Vixen Value of 24?
4th Lesson
Flabbergasted
If each number in a sequence must be a factor or multiple of the previous number what is the longest sequence that can be made from the given numbers?
5th Lesson
Word Difference
Can you find substitutions which will make the word sum correct?
6th Lesson
Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
