Trigonometry
Term 1 starting in week 4 :: Estimated time: 3 weeks
- Explore ratio in similar right-angled triangles
- Work fluently with the hypotenuse, opposite and adjacent sides
- Use the tangent ratio to find missing side lengths
- Use the sine and cosine ratio to find missing side lengths
- Use sine, cosine and tangent to find missing side lengths
- Use sine, cosine and tangent to find missing angles
- Calculate sides in right-angled triangles using Pythagoras' Theorem (review)
- Select the appropriate method to solve right-angled triangle problems
- Work with key angles in right-angled triangles
For higher-attaining pupils:
- Use trigonometry in 3-D shapes Use the formula ½ ab sin C to find the area of a triangle
- Understand and use the sine rule to find missing lengths
- Understand and use the sine rule to find missing angles
- Understand and use the cosine rule to find missing lengths
- Understand and use the cosine rule to find missing angles
- Choosing and using the sine and cosine rules
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
 Pythagoras Basics A drill and practice self marking exercise on the basics of Pythagoras' theorem.
Pythagoras Basics A drill and practice self marking exercise on the basics of Pythagoras' theorem. Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem.
Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem. Demonstrating Pythagoras Short clip from QI: Stephen Fry demonstrates Pythagoras' theorem.
Demonstrating Pythagoras Short clip from QI: Stephen Fry demonstrates Pythagoras' theorem. Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem.
Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem. Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.
Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides. Which Side? Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse.
Which Side? Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse. Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles.
Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles. Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.
Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.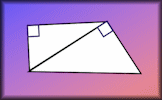 Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem
Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem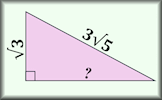 Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.
Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.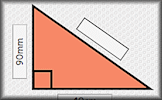 Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles.
Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles.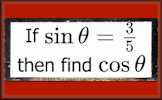 If Then Trigonometry Finding the exact values of sine, cosine and tangent of angles if given a different trig ratio.
If Then Trigonometry Finding the exact values of sine, cosine and tangent of angles if given a different trig ratio. Common Trig Ratios Video You may not realise that it is possible to find sin60° or tan45° without a calculator. This video is to help you do the online, self-marking exercise.
Common Trig Ratios Video You may not realise that it is possible to find sin60° or tan45° without a calculator. This video is to help you do the online, self-marking exercise.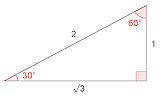 Common Trig Ratios Degrees A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles.
Common Trig Ratios Degrees A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles.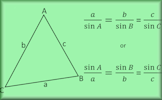 Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
Here are some exam-style questions on this topic:
- "\(ABC\) is a right-angled triangle." ... more
- "An isosceles triangle shaped frame is made from four pieces of metal. The frame has a height of 8 metres and a base of length 12 metres." ... more
- "Work out the value of \(x\), the length in centimetres of one of the sides of this right-angled triangle." ... more
- "ABC is a right-angled triangle as shown in the diagram below. Calculate the length of AB giving your answer correct to three significant figures." ... more
- "An arborist sights the top of a tree using a clinometer and reads the angle of elevation to be 29o. Her clinometer is 28 metres from the base of the tree and is on a tripod making it 1.5 metres above ground level." ... more
- "The diagram shows a right-angled triangle and a semicircle. The straight side of the semicircle is the same length as the longest side of the triangle." ... more
- "Here is triangle PQR:" ... more
- "The diagram shows a trapezium where the sides AC and BD are parallel." ... more
- "Four copies of a green right-angled triangle are used to enclose a yellow square." ... more
- "The area of the triangle is 10.6 cm2. Calculate the value of \(\sin {x}\)." ... more
- "Find the exact value of tan45° × sin30° × cos30°" ... more
- "The diagram shows a quadrilateral, ABCD, formed from two triangles, ABC and ACD." ... more
- "Consider the triangle ABC where AB=17cm, AC=14cm and the angle BAC = 118o. Find the length of BC." ... more
- "The angle marked \(x\) in the diagram below is obtuse. Find the value of \(x\)" ... more
- "The Tamarack triathlon race consists of swimming, cycling and running. Competitors swim from A to B, then cycle from B to C and finally run from C back to A." ... more
- "(a) Write down the exact value of \(\tan 60^o\)." ... more
- "Rectangle ABCD is the horizontal base of a trapezoidal prism ABCDEFGH." ... more
- "A triangular prism is made using two right-angled triangles and three rectangular pieces of cardboard. Five of the vertices have been labeled \(A, B, C, D \text{ and } E\) as shown in the photograph below." ... more
- "The area of triangle ABC (not drawn to scale) is " ... more
- "Four congruent triangles come together to make a square as shown in the diagram. The ratio of the area of one triangle to the area of the square is 1:5. Find the area of the square in square centimetres." ... more
- "The diagram shows the positions of three towns, Aberville (A), Buchus (B) and Clipton(C)." ... more
- "The diagram shows parallelogram ABCD in which AD = \(x\) cm, DE = 12 cm and angle ABC = 30°" ... more
- "In triangle ABC, AB = 7cm and AC = 9cm. The area of the triangle is 20cm2." ... more
- "The diagram shows a rectangular-based pyramid, TABCD (not drawn to scale)." ... more
- "ABC is a triangular car park on horizontal ground. The length of AB is 90m and the length of AC is 65m. The size of angle BCA is 68o." ... more
- "The diagram (not to scale) shows a quadrilateral made up of a number of triangles." ... more
- "Calculate the length of the side marked \(x\)." ... more
- "The diagram shows quadrilateral \(ABCD\) and is not drawn to scale." ... more
- "News is spreading of Pokémon sightings in Greenleaf Park. There is a Bulbasaur (B)on a bearing of 063o from Ayden and a Charmeleon (C) on a bearing of 110o from Ayden." ... more
- "In the diagram of triangle ABC (not to scale) D is a point on BC." ... more
- "The diagram, not drawn to scale, shows a quadrilateral ABCD." ... more
- "In the diagram above (not drawn to scale), AB=12mm, BC=8mm and angle ABC=123o" ... more
- "Two towers are situated close to each other on level ground. From point C on the ground directly between the two buildings, the angle of elevation to the top of each tower is \( \theta \)." ... more
- "The diagram below shows triangle ABC and the lengths of its sides. It is known that the cosine of angle \(C\hat{A}B\) is one third." ... more
- "Consider a triangle DEF, where DF= 15cm, FE = 9cm and EDF = 21°." ... more
- "The diagram shows quadrilateral ABCD." ... more
- "Christine owns a four sided piece of land shown in the diagram below as ABCD. The length of BC is 180 m, the length of CD is 70 m, the length of AD is 90 m, the size of angle BCD is 82° and the size of angle BAD is 102°. The diagram is not to scale" ... more
- "A builder marks out three points A, B and C on the ground such that AB = 11m , AC = 15m and angle BAC = 124o." ... more
- "Melissa has a webcam on the top of her computer screen. She has the zoom level adjusted so that that her head is framed nicely in the image produced. The diagram shows the setup." ... more
- "A drone flying test course is in the shape of a triangle, ABC, with AB = 400m , BC = 600m and angle ABC = 44o. The course starts and finishes at point A." ... more
- "The diagram shows a circle of radius 8.6cm with points ABCD on the circumference of the circle." ... more
- "Emma sails in a small dinghy from point A in a straight line to a buoy at point B. She is moving at an average speed of 19 km/h, for 6 minutes, on a bearing of 125°." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Pythagoras Pythagoras was a Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. He is most famous for his theorem connecting the lengths of the sides of right angled triangles. His theorem states that the squares of the lengths of the two shorter sides of any right-angled triangle will add up to the square of the length of the longest side (the hypotenuse). This theorem can be used to calculate the length of any side of a right-angled triangle if the lengths of the other two sides are known. Do you know when the next Pythagorean Day is? It will occur when the square of the day added to the square of the month equals the square of the last two digits of the year.
- Trigonometry Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Pupils begin by learning the names on the sides of a right-angled triangle relative to the angles. They then learn the ratios of the lengths of these sides and the connection these ratios have with the size of the angles. Having mastered right-angled triangle trigonometry pupils then progress to more advanced uses including the sine rule and cosine rules. The use of a scientific or graphing calculator is essential for this topic and correct, efficient use of the calculator is an important skill to develop. Here's a Trigonometry Wordsearch just for fun.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson

Spin the Wheel
Many basic numeracy questions generated from the number selected by the wheel of fortune.
2nd Lesson

Moon Lengths
Estimate the distances shown on this photograph of the moon's surface.
3rd Lesson

Number Recall
Can you improve your ability to remember telephone numbers?
4th Lesson

Vowelless
Vowels have been taken out of mathematical words. Can you recognise them?
5th Lesson

Pears Make Squares
Find three numbers such that each pair of numbers adds up to a square number.
6th Lesson

Only One Number
Find other numbers that can be changed to 1 on a calculator using only the 4 key and any operation.
7th Lesson

Missing Operations
Each red box represents a missing operation (+, -, x or ÷). Can you work out what they are?
8th Lesson

Siam Symbols
Can you work out what each of the strange symbols represents in these calculations?
9th Lesson

Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.

