Cookies are used on this website.

Activities for pupils

Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.

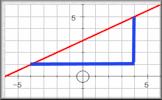• Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run.
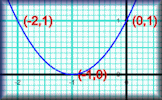• Plotting Graphs Complete a table of values then plot the corresponding points to create a graph.
• Straight Line Graphs Video After drawing a straight line graph learn about its equation in the form y = mx + c.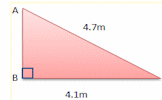
• Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem.
• Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem.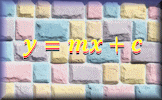
• Straight Line Graph Equation An online exercise about the equation y=mx+c and the features of a straight line graph.
• Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.
• Don's Graph Snaps Complete the tables and find the equations of the graphs that can be seen in the snaps.
• Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles.
• Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.
• Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function.
• Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem
• 3D Trigonometry Presentation A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes.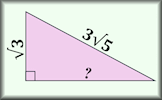
• Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.
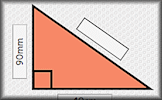• Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles.
• Graph Patterns Find the equations which will produce the given patterns of graphs.
• Three Dimensional Trigonometry Video When you have mastered trigonometry in two dimensions it is time to practise solving three-dimensional problems.
• Line Graph Challenge A challenge to produce the straight line patterns using a GDC or graph plotting software.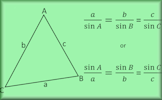
• Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
• Straight Line Graphs 10 straight line graph challenges for use with computer graph plotting software or a graphical display calculator.
• Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
• Name that Graph Choose from the given functions the one that best describes the shape of the graph.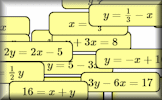
• Parallel Graphs Collect together in groups the equations of the graphs that are parallel to each other.
• Perpendicular Pairs Find the pairs of equations that will produce perpendicular graphs.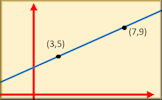
• Equation of a Line Through Points Match the equations of the straight line graphs to the clues about gradients and points.
• Equation of Line through Points Video A short video showing how to find the equation of a line that passes through given points.
• Origin of Degrees and Radians Exploring why a full rotation is 360 degrees and, why using radians can be a more useful alternative.
• Functions An online exercise on function notation, inverse functions and composite functions.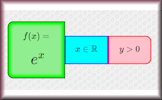
• Domain, Range and Asymptotes Match the functions with their features. A drag and drop activity.
• Coordinate Geometry Table Fill in the empty cells of this table with information about lines, gradients and coordinates.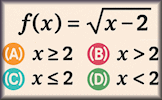
• Domain and Range Find the domain and range of various functions expressed in different ways

Here are some exam-style questions on this topic:

• "The equation of the line L₁ is \(y = 2 - 5x\)." ... more
• "Which of the following lines is parallel to the x-axis?" ... more
• "Show that line \(5y = 7x - 7\) is perpendicular to line \(7y = -5x + 55\)." ... more
• "An arborist sights the top of a tree using a clinometer and reads the angle of elevation to be 29^o. Her clinometer is 28 metres from the base of the tree and is on a tripod making it 1.5 metres above ground level." ... more
• "The diagram shows a right-angled triangle and a semicircle. The straight side of the semicircle is the same length as the longest side of the triangle." ... more
• "A straight line goes through the points \((a, b)\) and \((c, d)\), where" ... more
• "The diagram shows a trapezium where the sides AC and BD are parallel." ... more
• "The straight line \(L\) has the equation \(4y = 3x + 5\)." ... more
• "Taptaya Park Tower is over two hundred metres tall. There is a zip wire from the observation deck to a point on the ground 550 metres away in a northerly direction." ... more
• "Given the function:" ... more
• "The images below show a graphic display calculator screen with different functions displayed as graphs." ... more
• "Match the equation with the letter of its graph" ... more
• "Neung is at Bangkok's Suvarnabhumi Airport watching the planes take off. He observes a plane that is at an angle of elevation of 25^o from where he is standing at point N. The plane is at a height of 390 metres as can be seen in the following diagram (not to scale)." ... more
• "The graph of y = f(x) is drawn accurately on the grid." ... more
• "(a) A function is represented by the following function machine." ... more
• "Suppose a rhombus ABCD is drawn on a coordinate plane with the point A situated at (4,7). The diagonal BD lies on the line \(y = 2x - 5 \)" ... more
• "The Tamarack triathlon race consists of swimming, cycling and running. Competitors swim from A to B, then cycle from B to C and finally run from C back to A." ... more
• "Here is a function machine that produces two outputs, A and B." ... more
• "Rectangle ABCD is the horizontal base of a trapezoidal prism ABCDEFGH." ... more
• "The following diagram shows a circle with centre O and radius 9 cm." ... more
• "ABC is a triangular car park on horizontal ground. The length of AB is 90m and the length of AC is 65m. The size of angle BCA is 68^o." ... more
• "The diagram shows quadrilateral \(ABCD\) and is not drawn to scale." ... more
• "Consider the points A(-5, 15). B(4, 6) and C(-8, 12). The line \(L\) passes through the point A and is perpendicular to [BC]." ... more
• "The perimeter of the sector is 8 cm and the area of the sector is 3 cm²." ... more
• "The diagram shows a circle with a minor sector shaded blue and a major sector shaded yellow." ... more
• "The following diagram (not to scale) shows a circle with centre O and radius 7 cm." ... more
• "Part of the function of \(y=f(x)\) is shown in the following diagram." ... more
• "An astronaut measures the angle of elevation of a light on the surface of a mysterious sphere on a faraway planet." ... more
• "The following diagram shows part of a circle with centre O and radius 10cm." ... more
• "Two towers are situated close to each other on level ground. From point C on the ground directly between the two buildings, the angle of elevation to the top of each tower is \( \theta \)." ... more
• "The circumference of a given circle \(C\) can be represented by the function \(C(A) =2\sqrt{A \pi}, A \ge 0 \) where \(A\) is the area of the circle. The graph of the function \(C\) is shown for \(0 \le A \le 16\)." ... more
• "The diagram shows the graph of \(y=f(x)\), for \(-3\le x \le 4\)." ... more
• "The diagram below shows triangle ABC and the lengths of its sides. It is known that the cosine of angle \(C\hat{A}B\) is one third." ... more
• "Consider a triangle DEF, where DF= 15cm, FE = 9cm and EDF = 21°." ... more
• "A function is defined as \(f(x) = 2{(x - 3)^2} - 5\) ." ... more
• "The circumference of a given circle \(C\) can be represented by the function \(C(A) = 2 \sqrt{A \pi}\) , \(A \ge 0 \) , where \(A\) is the area of the circle. The graph of the function \(C\) is shown for \(0 \le A \le 10\)." ... more
• "Christine owns a four sided piece of land shown in the diagram below as ABCD. The length of BC is 180 m, the length of CD is 70 m, the length of AD is 90 m, the size of angle BCD is 82° and the size of angle BAD is 102°. The diagram is not to scale" ... more
• "A builder marks out three points A, B and C on the ground such that AB = 11m , AC = 15m and angle BAC = 124^o." ... more
• "The following diagram shows a semicircle with centre O. Points A. B and C lie on the circumference of the circle and AC is a diameter. Angle BOC = \(\theta\), where \(0 < \theta < \frac{\pi}{2}\)." ... more
• "An Asian water buffalo is tethered in a rectangular field by a rope of length \(r\) metres. One end of the rope is securely tied to point \(P\) as shown in this diagram (not drawn to scale)." ... more
• "A drone flying test course is in the shape of a triangle, ABC, with AB = 400m , BC = 600m and angle ABC = 44^o. The course starts and finishes at point A." ... more
• "Consider the function \(f(x) = k^x \) where \(x, k \in \mathbb{R}\) and \( x \gt 0, k > 1\)." ... more
• "Let \(f(x) = \frac{9x-3}{bx+9}\) for \(x \neq -\frac9b, b \neq 0\)." ... more
• "Emma sails in a small dinghy from point A in a straight line to a buoy at point B. She is moving at an average speed of 19 km/h, for 6 minutes, on a bearing of 125°." ... more
• "A function \( g \) is defined by \( g(x) = \frac{3x - 10}{x^2 - 9} \), where \( x \in \mathbb{R} \), \( x \neq \pm3 \)." ... more

See all these questions

Here are some Advanced Starters on this statement:

• Catering for a Function
  Find f(x) given f(x-1). more
• GDC Challenge
  Produce the given graph on a graphic display calculator more
• Parallel Graphs
  Determine from their equations which of the straight line graphs are parallel and perpendicular. more
• Pizza Slice
  A problem which can be solved by considering the areas of a triangle and a sector of a circle. more
• Speed Circles
  Find the diameters of the circles in the corners of the square. more
• Tan 22.5
  Find an exact value for tan 22.5° without using a calculator. more
• Three Right Triangles
  Calculate the lengths of the unlabelled sides of these right-angled triangles. more
• Trig Blot
  Find all the measurements of the given triangle. more
• Venn Graphs
  Type the equation of a graph into each section of the Venn diagram. more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Angles Pupils should understand that angles represent an amount of turning and be able to estimate the size of angle. When constructing models and drawing pupils should be able to measure and draw angles to the nearest degree and use appropriate language associated with angles. Pupils should know the angle sums of polygons and that of angles at a point and on a straight line. They will learn about angles made in circles by chords, radii and tangents and recognise the relationships between them. Pupils will work with angles using trigonometry, transformations and bearings. In exams pupils are often instructed that while non-exact answers should be given to three significant figures, angle answers should be given to one decimal place.
• Functions A relationship between two sets can be called a mapping. Elements of the first set (domain) are mapped to elements of the second set (range). A function is a special type of mapping for which one value in the domain maps to one, and only one value in the range.Pupils in Primary school will use the concept of function machines to perform calculations. They will then learn to ‘work backwards’ to find the inverse function. The study of functions becomes more formal as pupils become more proficient and able to cope with more complex mathematical ideas.
• Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
• Trigonometry Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Pupils begin by learning the names on the sides of a right-angled triangle relative to the angles. They then learn the ratios of the lengths of these sides and the connection these ratios have with the size of the angles. Having mastered right-angled triangle trigonometry pupils then progress to more advanced uses including the sine rule and cosine rules. The use of a scientific or graphing calculator is essential for this topic and correct, efficient use of the calculator is an important skill to develop. Here's a Trigonometry Wordsearch just for fun.