1
Can you figure out what equations we used to produce the pattern above? Type your answers below.
This graph plotting challenge is intended to familiarise students with the equation of a straight line. There are five challenges each with between three and six straight lines in a pattern. In order to proceed to the next challenge the correct equation should be entered into the boxes provided.
|
The equation of any straight line can be written in the form: y = mx + cwhere m is the gradient of the line and c is the y-coordinate of the point where the line crosses the y-axis (y-intercept). The gradient of the line can be found by considering to points on the line where the exact coordinates can be determined. The rise is the vertical distance between these points and the run is the hirizontal distance. The gradient is the rise divided by the run (rise over run). If the line slopes from bottom left to upper right the gradient is positive. If the line slopes from top left to bottom right the gradient is negative. |
 |
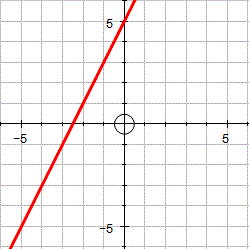For example the graph shown to the left has a gradient of 2 (for every one square across the line goes up two squares. Rise over run is 2 over 1 which is 2.) The y-intercept is 5 so the equation is: y = 2x + 5A horizontal line with a y-intercept of three has equation: y = 3A vertical line with an x-intercept of three has equation: x = 3 |
For Whole ClassStraight Line Graphs 10 straight line graph challenges for use with computer graph plotting software or a graphical display calculator. |
RelatedGraph Match Match the equations with the images of the corresponding graphs. Linear, quadratic and more. |
Just For FunHuman Graphs Students should be encouraged to stand up and make the shapes of the graphs with their arms. |
SuggestedPlotting Graphs Complete a table of values then plot the corresponding points to create a linear, quadratic or reciprocal graph. |
The solutions to this and other Transum puzzles, exercises and activities are available in this space when you are signed in to your Transum subscription account. If you do not yet have an account and you are a teacher or parent you can apply for one here.
A Transum subscription also gives you access to the 'Class Admin' student management system and opens up ad-free access to the Transum website for you and your pupils.
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
The graph plotting software used in this page was adapted from code written by Richard Ye | GitHub Development (version 0.4)
