Ratio and fractions
Term 2 starting in week 7 :: Estimated time: 2 weeks
- Compare quantities using a ratio (review)
- Link ratios and fractions (review)
- Share in a ratio (given total or one part) (review)
- Use ratios and fractions to make comparisons
- Link ratios and graphs (review)
- Solve problems with currency conversion
- Link ratios and scales (review)
- Use and interpret ratios of the form \(1 : n\) and \(n : 1\)
- Solve 'best buy' problems
- Combine a set of ratios
- Link ratio and algebra
- Mixed ratio problems
For higher-attaining pupils:
- Ratio in area problems
- Ratio in volume problems
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
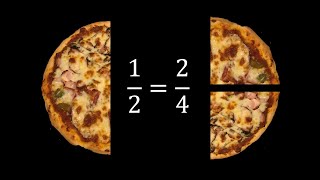Equivalent Fractions Video Learn about equivalent fractions and how to express fractions in their lowest terms.
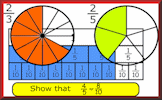Equivalent Fractions Practise finding equivalent fractions numerically and in fraction diagrams.
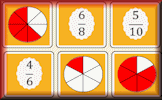Equivalent Fraction Pairs The traditional pairs or Pelmanism game adapted to test knowledge of equivalent fractions.
Express as a Fraction Express one quantity as a fraction of another, where the fraction could be less than 1 or a mixed number.
Ratio A self marking exercise on using ratio notation, reducing a ratio to its simplest form and dividing a given quantity into a number of parts in proportion to a given ratio.
Double, Double, Halve and Treble Questions about scaling up the ingredients in the correct proportion for the witch's brew at Hallowe'en.
Ratio Video Learn to work with ratios including dividing a quantity in a given ratio.
Dividing in a Ratio A slide presentation showing how to divide a quantity in a given ratio
Ratios vs Fractions Relate the language of ratios and the associated calculations to the arithmetic of fractions.
Scale Drawings Measure line segments and angles in geometric figures, including interpreting scale drawings.
Construct a congruent triangle Construction (with compass and straight edge) of a triangle congruent to a given triangle.
Recipe Ratios Learn the mathematics required to adapt recipes to serve a different number of people.
Unit Pricing Calculate the unit cost of items to earn jigsaw pieces that make a joke.
Map Scales Video Refresh your understanding of map scales expressed as ratios.
Map Scales Test your understanding of map scales expressed as ratios with this self marking quiz.
Ratio Clues Arrange the ratio clues in the clouds in a logical order to work out the values of the twelve letters.
Congruent Triangles Video Learn the conditions for two triangles to be congruent and then use this information to solve problems.
Congruent Triangles Test your understanding of the criteria for congruence of triangles with this self-marking quiz.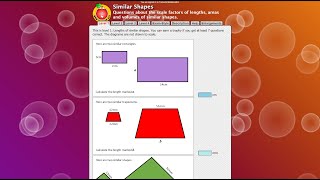
Scale Factors Video The scale factor, area factor and volume factor of similar shapes are quite different.
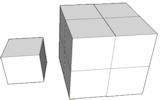Similar Shapes Questions about the scale factors of lengths, areas and volumes of similar shapes.
Here are some exam-style questions on this topic:
- "If A is 150% more than B, what is the ratio A:B?" ... more
- "At a concert, the number of men, women and children can be expressed with the following ratio:" ... more
- "Toystore sell model sheep in four different colours. In their newest warehouse there are currently 1760 sheep in stock. Three eighths of the sheep are yellow, 15% of the sheep are blue and the ratio of green to red sheep is 5:6." ... more
- "A triangle, ABC, is drawn (not to scale) with AC = 12.6 cm." ... more
- "In January, a supermarket sold 12 624 boxes of breakfast cereal." ... more
- "(a) Audrey, Seymore and Mr Mushnic share potted plants in the ratio Audrey : Seymore : Mr Mushnic = 3 : 4 : 7. Seymore receives 12 plants. Calculate the total number of plants shared." ... more
- "Rishi breeds fish in tanks. Some of the tanks are small and some are large." ... more
- "(a) Victor estimates the height of a flag pole by holding a ruler vertically so the height of the flag pole is exactly covered by the ruler when he is standing 240 centimetres from the flag pole." ... more
- "Prove that triangle ABC is congruent to triangle CDA if ABCD is a parallelogram." ... more
- "Promise is going to make some chocolate pyramids to sell." ... more
- "£580 is shared between Alice, Bally, Chris and Dean." ... more
- "ABCD is a parallelogram with diagonals meeting at E. Prove that triangle ABE is congruent to triangle CDE." ... more
- "Triangle JKL is the cross-section of a prism of length 25cm." ... more
- "A shop sells mini packs of fruit gums of different sizes" ... more
- "The circumference of the red circle is 80% of the circumference of the blue circle." ... more
- "The ratio a : b is equivalent to the ratio 7 : 3 and 8b = 5c" ... more
- "(a) Find the ratio \(a:b \) given the equation:" ... more
- "(a) Find the area of a regular octagon if the distance from its centre to any vertex is 10cm." ... more
- "At a summer camp the campers can choose one of three programmes: camp craft, water sports or hiking." ... more
- "The three boxes pictured below are mathematically similar." ... more
- "There are some round counters and some square counters in a pot. The counters are either blue or green." ... more
- "The points A, B C and D lie in order on a straight line." ... more
- "ABC is an isosceles triangle in which AB = AC." ... more
- "Two similar pentagonal based pyramids have surface areas 200 cm2 and 50 cm2 respectively." ... more
- "A fishing boat is somewhere along the line from A to C." ... more
Here are some Advanced Starters on this statement:
- Hundred and Fifty Percent
Divide 110 into two parts so that the larger part is 150% of the smaller part. more - Square in Rectangle
Find the area of a square drawn under the diagonal of a rectangle more - Three Right Triangles
Calculate the lengths of the unlabelled sides of these right-angled triangles. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Fractions A fraction is a part of a number. Fractions are either vulgar or decimal. Vulgar fractions can be proper, improper or mixed. Equivalent fractions have the same value. Pupils, at all stages of their learning, should practise using fractions. From dealing with halves, the most basic fraction, to manipulating algebraic fractions containing surds, this topic is always relevant. Proficiency also depends on reasonable numeracy skills particularly the multiplication tables and finding the lowest common multiple of two numbers. Pupils also need to be able to convert vulgar fractions to decimals and percentages and vice versa. Be wary of teaching the 'rules' for manipulation fractions by rote. Pupils need to understand the reason why and the time-honoured key to understanding starts with the imaginary pizza and the much-used fraction wall.
- Ratio A ratio is a relationship between two numbers of the same kind. In layman's terms a ratio represents, simply, for every amount of one thing, how much there is of another thing. This topic presents a number if different ways pupils can represent ratios and apply their meaning to problem solving situations.
- Shape This topic is aimed at the learners of basic geometry, which is the study of size, shape and position. More than other areas of mathematics this topic helps pupils to learn about the definitions and properties of basic shapes. There are many activities provided ranging from simple shape naming games to applying more advanced formulas and theorems. The most popular activities however are those involving pupils to count the number of triangles or rectangles in patterns and come up with effective strategies and justifications for their answers. The work pupils produce for this topic can make very good display material. The use of colour can enhance the diagrams and make the learning environment more conducive to study. There are many connections between the mathematics of shape and Art. There are fascinating works of art based on symmetry, tessellations and transformations.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Aunty Dotty
A real life situation requiring the division an amount of money according to a given ratio.
2nd Lesson
Plant More Trees
If six girls can plant 90 trees in a day. How many trees can ten girls plant in a day? The unitary method.
3rd Lesson
Word Search
Create your own mathematical word search for the whole class to enjoy.
4th Lesson
Targets
Use the given numbers to produce a calculation to get as close as possible to the given target.
5th Lesson
Scaramouche
Can you work out from the five clues given what the mystery number is?
6th Lesson
Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
