Using graphs
Term 1 starting in week 5 :: Estimated time: 2 weeks
- Reflect shapes in given lines (review)
- Construct and interpret conversion graphs (review)
- Construct and interpret other real-life straight line graphs (review)
- Interpret distance/time graphs
- Construct distance/time graphs
- Construct and interpret speed/time graphs
- Construct and interpret piece-wise graphs
- Recognise and interpret graphs that illustrate direct and inverse proportion
- Find approximate solutions to equations using graphs
For higher-attaining pupils:
- Estimate the area under a curve
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
 Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run.
Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run. Graph Paper Flexible graph paper which can be printed or projected onto a white board as an effective visual aid.
Graph Paper Flexible graph paper which can be printed or projected onto a white board as an effective visual aid. Plotting Graphs Complete a table of values then plot the corresponding points to create a graph.
Plotting Graphs Complete a table of values then plot the corresponding points to create a graph. Deconstructing Graphs Fill in the tables of values from the information that can be read from the given graphs.
Deconstructing Graphs Fill in the tables of values from the information that can be read from the given graphs.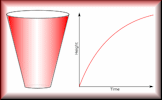 Fill Graph Pairs If the container is gradually filled with a steady flow of water which height-time graph would be produced?
Fill Graph Pairs If the container is gradually filled with a steady flow of water which height-time graph would be produced?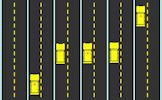 Helicopter View An animated introduction to distance-time graphs. Arial photographs of vehicles moving along a road placed side to side form a graph.
Helicopter View An animated introduction to distance-time graphs. Arial photographs of vehicles moving along a road placed side to side form a graph. Travel Graphs Video Learn about distance-time graphs, speed-time graphs and how to interpret them.
Travel Graphs Video Learn about distance-time graphs, speed-time graphs and how to interpret them.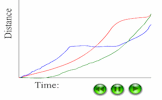 Hurdles Race An animated distance time graph to be viewed while a student interprets the graph and comments on the race that produced the graph.
Hurdles Race An animated distance time graph to be viewed while a student interprets the graph and comments on the race that produced the graph.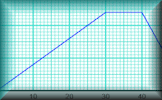 Travel Graphs Test your understanding of distance time graphs and speed time graphs (velocity time graph) with this self-marking exercise.
Travel Graphs Test your understanding of distance time graphs and speed time graphs (velocity time graph) with this self-marking exercise. Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Here are some exam-style questions on this topic:
- "At depths below 900 metres, the temperature of the water in the sea is given by the formula:" ... more
- "The graph gives information about how the charging time in hours of an electric car relates to its range given as a distance in kilometres." ... more
- "Lyana has drawn a time series graph to show the number of minutes she spent doing homework on some of the days in June 2021." ... more
- "The graph shows the height of water in a container over a period time during which the water enters the container at a constant rate." ... more
- "The diagram is of a container which is filled with water entering at a constant rate." ... more
- "The following diagram shows a distance-time graph of the movement of a fish." ... more
- "Marilou and Sam had a skiing race. Here is Marilou’s speed-time graph from the start of the race." ... more
- "(a) Sketch a graph on the axes below left that shows that \(y\) is directly proportional to \(x\)." ... more
- "At a constant temperature, the volume of a gas \(V\) is inversely proportional to its pressure \(p\). By what percentage will the pressure of a gas change if its volume increases by 15% ?" ... more
- "Here is a speed-time graph for a drone." ... more
- "A model train is placed on a length of straight track." ... more
- "The diagram shows the speed-time graph of part of my cycle journey one morning. The speed is given in kilometers per hour but the time is given in minutes." ... more
- "A motorbike moves from rest along a straight road. The graph below shows the speed, \(v\) in metres per second of the motorbike \(t\) seconds after it started to move." ... more
- "The graph shows the temperature (\(T\)) of an unidentified flying object over a period of 10 seconds (\(t\))." ... more
- "(a) Sketch the graph of \( y = f(x) \) for values of \( x \) between \(-5\) and \(5\) given that:" ... more
- "The graph shows the distance travelled, in metres, of a commuter train as it pulls out of a station." ... more
- "Here is a speed-time graph for a go kart." ... more
- "The diagram shows the graph of \( y = f(x) \) for \( -2.1 \leq x \leq 2 \). The y axis is vertical and the x axis is horizontal." ... more
Here are some Advanced Starters on this statement:
- Average Cycling Speed
Work out the average speed of two journeys. The obvious answer is not the correct answer. more - Temperature Sum
Can you explain why 0oC + 0oC does not equal 64oF more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
- Statistics Statistics is the study of the collection, organisation, analysis, interpretation and presentation of data. It deals with all aspects of data, including the planning of data collection in terms of the design of surveys and experiments. It also includes describing mathematical relationships between variables and presenting these to an audience in a way that best conveys meaning. See also the topics called Data Handling, Probability and Averages.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Reflective Cat
On squared paper copy the drawing of the face then reflect it in three different lines.
2nd Lesson

Book Worm
Work out the distance the book worm needs to eat through to get to the back cover of the last book.
3rd Lesson
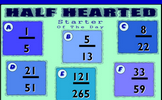
Half Hearted
Find the number which when added to the top (numerator) and bottom (denominator) of each fraction make it equivalent to one half.
4th Lesson

Kim's Game 1
This is the Maths version of the traditional memory game. Memorise 10 mathematical facts then recall them as they disappear from view.
5th Lesson

Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
6th Lesson

All for 100
Can you write an ex
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.

