Gradients and lines
Term 1 starting in week 1 :: Estimated time: 2 weeks
- Equations of lines parallel to the axis (review)
- Plot straight line graphs (review)
- Interpret \(y = mx + c\) (review)
- Find the equation of a straight line from a graph (review)
- Equation of a straight-line graph given one point and gradient
- Equation of a straight-line graph given two points
- Determine whether a point is on a line
- Solve linear simultaneous equations graphically (review)
For higher-attaining pupils:
- Recognise when straight lines are perpendicular
- Find the equations of perpendicular lines
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run.
Straight Line Graphs Video After drawing a straight line graph learn about its equation in the form y = mx + c.
Simultaneous Shopping Find the cost of the individual items in shopping baskets (introduction to simultaneous equations).
Superfluous Find a strategy to figure out the values of the letters used in these calculations.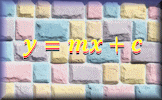
Straight Line Graph Equation An online exercise about the equation y=mx+c and the features of a straight line graph.
Don's Graph Snaps Complete the tables and find the equations of the graphs that can be seen in the snaps.
Simultaneous Equations Video Learn to solve simultaneous equations from the very basic to those containing quadratics. This video is to help you do the online, self-marking exercise.
Simultaneous Equations A self-marking, multi-level set of exercises on solving pairs of simultaneous equations.
Graph Patterns Find the equations which will produce the given patterns of graphs.
Simultaneous Solutions Arrange the given pairs of simultaneous equations in groups to show whether they have no solution, one solution or infinite solutions.
Unbeknownst Some picture grid puzzles which can be solved by using simultaneous equations.
Line Graph Challenge A challenge to produce the straight line patterns using a GDC or graph plotting software.
Straight Line Graphs 10 straight line graph challenges for use with computer graph plotting software or a graphical display calculator.
Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.
Equation of a Line Through Points Match the equations of the straight line graphs to the clues about gradients and points.
Equation of Line through Points Video A short video showing how to find the equation of a line that passes through given points.
Coordinate Geometry Table Fill in the empty cells of this table with information about lines, gradients and coordinates.
Here are some exam-style questions on this topic:
- "The equation of the line L1 is \(y = 2 - 5x\)." ... more
- "René chooses two points at random on a sheet of graph paper by throwing two dice twice. He labels the points \(R\) and \(D\)." ... more
- "Nora and Dora are trying to solve the following simultaneous equations by finding the intersection of their graphs." ... more
- "Which of the following lines is parallel to the x-axis?" ... more
- "Show that line \(5y = 7x - 7\) is perpendicular to line \(7y = -5x + 55\)." ... more
- "A straight line goes through the points \((a, b)\) and \((c, d)\), where" ... more
- "The straight line \(L\) has the equation \(4y = 3x + 5\)." ... more
- "(a) Use the red graphs to solve the simultaneous equations:" ... more
- "The straight line \(y = 3x - 4\) intersects the curve \(y = x^2 + 4x – 7\) at the points \(A\) and \(B\)." ... more
- "Solve the simultaneous equations" ... more
- "A is the point (-5, -9) and B is the point (10, 1)." ... more
- "Estimate the solutions of the following simultaneous equations using their graphs as drawn on the grid below." ... more
- "Solve the simultaneous equations:" ... more
- "A rectangular sheet of paper can be cut into two identical rectangular pieces in two different ways, either by cutting along line A or by cutting along line B." ... more
- "Show that you understand equations and inequalities by answering the following:" ... more
- "Draw the graph of \(y = 2x^2 + 3x - 7\) for \( -3.5 \le x \le 2\). Draw suitable straight lines to find approximate solutions (to one decimal place) of the equations:" ... more
- "Suppose a rhombus ABCD is drawn on a coordinate plane with the point A situated at (4,7). The diagonal BD lies on the line \(y = 2x - 5 \)" ... more
- "Solve algebraically the simultaneous equations to find the solution where \(-10 \le x \le 10\)." ... more
- "Two numbers are chosen so that the sum of their squares is 25." ... more
- "The prices of two watches are in the ratio \(a:b\)." ... more
- "Consider the points A(-5, 15). B(4, 6) and C(-8, 12). The line \(L\) passes through the point A and is perpendicular to [BC]." ... more
- "The vertices of quadrilateral ABCD are A (2, 4), B (-1, 5), C (–3, 4) and D (–2, 2)." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
- Simultaneous Equations This topic covers simultaneous equations with two different variables. The starters pose real world problems which can be solved using the techniques taught at school or by other intuitive methods. Though there are many formal strategies for solving simultaneous equations the skill of forming the equations from real life situations is a very important stage in working towards a solution. Algebraic methods are the most efficient for solving basic simultaneous equations but graphical methods, probably using a graphic display calculator or computer software package, may be more suitable for less standard sets of simultaneous equations.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Suko
Interactive number-based logic puzzle similar to those featuring in The Times and Telegraph newspapers.
2nd Lesson
Stair Perimeter
Use the information implied in the diagram to calculate the perimeter of this shape.
3rd Lesson
Unmagic Square
Arrange the numbers 1 to 9 in a 3 by 3 grid so that none of the line totals are the same.
4th Lesson
Anagrams
Can you un-jumble these mathematical words?
5th Lesson
Dice Nets
Determine whether the given nets would fold to produce a dice.
6th Lesson
Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
