Working with circles
Term 2 starting in week 3 :: Estimated time: 2 weeks
- Recognise and label parts of a circle (review)
- Calculate fractional parts of a circle
- Calculate the length of an arc
- Calculate the area of a sector
- Understand and use the volume of a cylinder and cone
- Understand and use the volume of a sphere
- Understand and use the surface area of a sphere
- Understand and use the surface area of a cylinder and cone
For higher-attaining pupils:
- Circle theorem: Angles at the centre and circumference
- Circle theorem: Angles in a semicircle
- Circle theorem: Angles in the same segment
- Circle theorem: Angles in a cyclic quadrilateral
- Solve area and volume problems involving similar shapes
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Circle Pairs Find the matching pairs of circle diagrams and circle properties in this interactive online game.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Circle Parts Kim's Game A memory game to be projected to help the whole class revise the names for the parts of a circle.
Circles Area and Circumference Video The circumference and area of a circle can be found if the radius or diameter are known.
Circles Practise using pi to calculate various circle measurements. There are six levels of difficulty.
Angle Theorem Kim's Game A memory game to be projected to help the whole class revise the circle angle theorems.
Circle Theorems Exercise Show that you understand and can apply the circle theorems with this self marking exercise.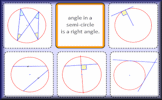
Circle Theorem Pairs A pairs game based around ten theorems about the angles made with chords, radii and tangents of circles.
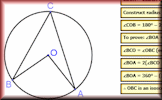Proof of Circle Theorems Arrange the stages of the proofs for the standard circle theorems in the correct order.
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.
Geometry Toolbox Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.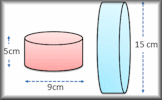
Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Here are some exam-style questions on this topic:
- "The diagram shows a water tank in the shape of a cylinder. It has a diameter of 76cm anf a height of 36cm." ... more
- "The diagram shows a right-angled triangle and a semicircle. The straight side of the semicircle is the same length as the longest side of the triangle." ... more
- "The points B, C, D, E and F are on a circle. DAE and CAB are straight lines and AB= BE." ... more
- "The points B, C, D and E lie on the circle with centre at A." ... more
- "Babatunde has to paint four containers." ... more
- "The diagram show a solid cone painted two different colours." ... more
- "A builder needs to lift a steel block. It is a cuboid with dimensions 2 m by 0.2 m by 0.2 m. Steel has a density of 7.6 g/cm3." ... more
- "The diagram shows a sector of a circle, centre O, with one angle shown as being 110°. If the radius of the circle is 8cm calculate:" ... more
- "[The surface area of a sphere of radius \(r\) is \(4\pi r^2\) and the volume is \(\frac43\pi r^3\)]" ... more
- "A circular dart board has radius of 30 cm." ... more
- "The diagram, not drawn to scale, shows the plan for a large, three dimensional sign which has been ordered to hang outside an ice cream shop." ... more
- "A yellow equilateral triangle has been painted on a purple sector. The side OC is 20cm and OA is 12cm. Calculate the area of the purple region ABCD as a percentage of the area of the whole sector OCD." ... more
- "The illustration shows a greenhouse in the shape of a pentagonal prism. The front of the greenhouse is a pentagon with a single line of symmetry. The sides of the greenhouse are vertical." ... more
- "B, C, D and E are points on the circumference of a circle, centre O." ... more
- "Points B, D, G and F lie on a circle." ... more
- "The diagram shows a sector of a circle with sector angle 160° and radius 18 cm." ... more
- "In the diagram above, not drawn to scale, A, B and C are points on a circle, centre O. TA is a tangent to the circle at A and OBT is a straight line. AC is a diameter and angle OTA = 28°." ... more
- "A circle is drawn inside a square so that it touches all four sides of the square." ... more
- "OAB is a sector of a circle with centre O and radius 10 cm." ... more
- " " ... more
- "Twenty four spherical shaped chocolates are arranged in a box in four rows and six columns." ... more
- "The three sides of an equilateral triangle are tangents to a circle of radius \(r\) cm. The sides of the triangle are each 10cm long." ... more
- "(a) Find \(x\), the size of angle ABC if B, C and D are all points on the circle to which AB is a tangent. The diagram is not drawn to scale." ... more
- "Three crayons are held together with an elastic band. The diagram below shows the end of the crayons and the elastic band." ... more
- "The diagram shows a circle with its centre at the origin." ... more
- "The diagram, not drawn to scale, shows chords joining points on the circumference of a circle. Prove that triangle ADE is similar to triangle BCE." ... more
- "The following diagram shows a circle with centre O and radius 9 cm." ... more
- "The diagram shows a rectangular-based pyramid, TABCD (not drawn to scale)." ... more
- "The diagrams are not drawn to scale" ... more
- "Two identical small yellow circles are drawn inside one large circle, as shown in the diagram. The centres of the small circles lie on the diameter of the large circle. The part of the large circle that is outside both small circles is painted red." ... more
- "The volume of a cone can be calculated using the formula \(V=\frac13 \pi r^2 h \) and the area of the curved surface of a cone can be calculated using \(A= \pi r l\) (where \(r\) is the radius and \(l\) is the slant height)." ... more
- "The diagram shows a water tank in the shape of a trapezoidal prism." ... more
- "A metal sphere has a radius 7.2 cm." ... more
- "A solid metal cylinder has a base radius of 5cm and a height of 9cm." ... more
Here are some Advanced Starters on this statement:
- Cuboid
Find the dimensions of a cuboid matching the description given more - Find The Radius
Find the radius of the circle from the small amount of information provided. more - Pizza Slice
A problem which can be solved by considering the areas of a triangle and a sector of a circle. more - Sphere Hole
Find the volume of the remaining part of a sphere after a 10cm cylindrical hole has been drilled through it. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Circles This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation. Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations. More mathematics related to the circle can involve angle theorems, loci and algebra.
- Mensuration Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume. It is linked closely to the topic of Estimation and related to the topics of Angles, Shape and Shave (3D). It is essential for pupils to have an understanding of the units used to measure which include both the more common metric units and the Imperial units still in common usage. We have found a good teaching strategy is to ask each of the pupils to "Bring to the next Maths lesson some visual aid which will help the rest of the class remember the size of a unit of measurement". See Memorable Measures below for the printable resources. This activity provides an association with a unit, a visual aid and a known person which is a great memory enhancer.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Pi Day
March 14th is Pi Day. The third month and the 14th day relates to 3.14 which is pi to three significant figures. How many figures of pi can you memorise?
2nd Lesson
Leap Year
A question about the birthdays of a child born on the 29th February.
3rd Lesson
On The Double
Double the numbers given in the table.
4th Lesson
One Digit 100
How many ways can you write an expression for 100 which only uses the same digit repeated and any operations?
5th Lesson
Plus
A number puzzle suitable for children with a wide range of abilities.
6th Lesson
Polygon Riddle 3
A 'My first is in...' riddle that describes a geometrical shape. Can you construct it?
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
