Non-calculator methods
Term 3 starting in week 7 :: Estimated time: 2 weeks
- Mental/written methods of integer/decimal addition and subtraction (review)
- Mental/written methods of integer/decimal multiplication and division (review)
- The four rules of fraction arithmetic (review)
- Exact answers
- Rounding to decimal places and significant figures (review)
- Estimating answers to calculations (review)
- Understand and use limits of accuracy
- Use number sense
- Solve financial maths problems
- Break down and solve multi-step problems
For higher-attaining pupils:
- Rational and irrational numbers (convert recurring decimals here)
- Understand and use surds
- Calculate with surds
- Upper and lower bounds
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Addition Video A reminder of how to add two or more numbers using the column method.
Basic Addition A self-marking exercise on addition with increasing levels of difficulty.
Number Line Banner A printable banner (multiple A4 sheets) of a colourful number line for the classroom wall.
Number Line This number line visual aid is designed to be projected onto a whiteboard for whole class exposition.
Decimals Line A number line showing tenths and hundredths with draggable arrows. This is a visual aid designed to be projected onto a whiteboard for whole class exposition
Formal Written Methods Examples of formal written methods for addition, subtraction, multiplication and division.
Rounding Ten Round the numbers to the nearest whole number or the given power of ten.
Decimal Plus Video Learn the written methods for adding and subtracting decimal numbers. This video is to help you do the online, self-marking exercise.
Beat The Clock It is a race against the clock to answer 30 mental arithmetic questions. There are nine levels to choose from.
Fractions Video So many people can't remember how to add, subtract, multiply and divide fractions so here is a reminder.
Discombobulated A fun game requiring you to find numbers which add up to the target number as quickly as possible.
Arithmagons Find the missing numbers in these triangular, self-checking puzzles and discover the wonders of these fascinating structures.
Decimal Plus Practise mental and written methods for adding and subtracting decimal numbers.
Multiplying and Dividing Decimals A straight forward, no nonsense demonstration of the methods of multiplying and dividing decimals.
Fractions A series of self-marking exercises on adding, subtracting, multiplying and dividing fractions.
Boxed In Fractions The classic dots and boxes two-player game with the addition of some fractions which determine your score.
Fractionagons Calculate the missing fractions in these partly completed arithmagon puzzles.
Rounding Video A reminder of how to round numbers to significant figures, decimal places and to the nearest power of ten.
Negative Numbers Use negative numbers in basic arithmetic and algebraic calculations and word problems.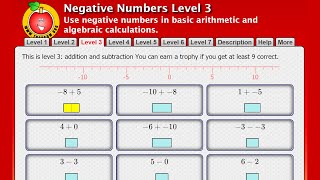
Negative Numbers Video Revise how to add, subtract, multiply and divide negative numbers.
Rounding DP A self marking exercise requiring students to round numbers to a given number of decimal places.
Rounding SF A self marking exercise requiring students to round numbers to a given number of significant figures.
Multi-step Problems Solve multi-step problems in contexts, deciding which operations and methods to use and why.
Mixed Numbers Revise the methods for adding, subtracting, multiplying and dividing mixed numbers (fractions) by watching this video.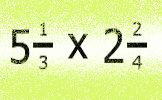
Mixed Numbers A self marking quiz about the application of the four operations to mixed numbers.
Numbasics A daily workout strengthening your ability to do the basic mathematical operations efficiently.
Rounding Snap If the last card put down equals the previous card to the nearest whole number then all players race to shout SNAP!
Number Skills Inventory A checklist of basic numeracy techniques that every pupil should know.
Thai Restaurant Calculate the restaurant bills for each of the tables in the Thai Restaurant.
Powten Practise multiplying and dividing by powers of ten without using a calculator.
Quickulations A mental arithmetic visual aid that displays random calculations then after a few seconds displays the answers.
Money Maths Test your skills and understanding with this online exercise about Money Maths and Personal Finance.
Rough Answers An exercise on rounding values in a calculation to find an approximate estimate of the answer.
Bidmaze Find your way through the maze encountering mathematical operations in the correct order to achieve the given total.
Expedite Drag the numbered cards to produce a multiplication fact. Complete twenty mixed times tables questions to earn a trophy.
Recurring Decimals Change recurring decimals into their corresponding fractions and vica versa.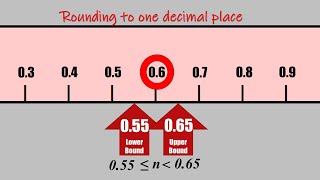
Upper and Lower Bounds Video A reminder of how to find the limits of accuracy of rounded values.
Upper and Lower Bounds Determine the upper and lower bounds when rounding or truncating quantities used in calculations.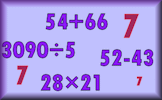
Heptaphobia Research Use written methods to answer ten arithmetic questions. When you have finished you will find the results of this amazing research.
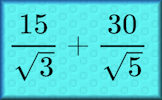Surds A self-marking exercise on calculating, simplifying and manipulating surds (also known as radicals).
Here are some exam-style questions on this topic:
- "A number, \(n\), when rounded to two decimal places is 7.32" ... more
- "The Glacier Ski Resort has this sign showing the safety limit for each cable car:" ... more
- "Without using your calculator, work out the value of the following calculations giving each answer as a fraction in its lowest terms. You must show all your working.
(a)
" ... more - "Work out the value of the following giving your answer to three significant figures:" ... more
- "A number, \(n\), is rounded to 2 decimal places." ... more
- "Ayden is marking out the pitch for a ball game in a large field." ... more
- "The height of a tree is 9 metres to the nearest metre." ... more
- "(a) Work out an estimate for the value of \( \sqrt{48.3 \times 82.01}\)." ... more
- "Find the product of the two numbers below giving your answer as a mixed number in its simplest form." ... more
- "Ralph used his calculator to work out the value of C, the circumference of a circle. Unfortunately he put his banana down on his desk so that it covered most of the calculator screen. All that can be seen are the first two digits of the answer." ... more
- "Minerva's Revenge, the longest rollercoaster in the Funville Theme Park, takes 95 seconds (to the nearest 5 seconds) to complete one circuit of the 2280 metre long track." ... more
- "Calculate the upper bound for the length of an edge of the cube if the long diagonal (connecting opposite vertices) is 62 metres correct to the nearest metre. You must show all your working." ... more
- "(a) Calculate the upper bound for the value of A giving your answer correct to 6 significant figures if:" ... more
- "Unit fractions have numerators equal to 1, for example \(\dfrac12\),\(\dfrac19\) and \(\dfrac{1}{36}\)." ... more
Here are some Advanced Starters on this statement:
- Fermi Problem
The classic Fermi problem using standard estimation techniques more - Four Fraction Division
Explain why the answer to a series of fraction divisions is a whole number. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Approximation Approximating a quantity is often to get a value that is easier to use or understand, at the cost of making it less precise. This approximation is very important in dealing with answers to mathematical problems and making them relevant to the real world. Rounding to a given number of decimal places or significant figures is required of pupils. The error introduced when approximating a value may be further magnified with subsequent calculations. Understanding this error and how it can be minimised is another important aspect of this topic. See also the "Rounding" and "Estimating" Topic pages.
- Arithmetic The ability to perform mathematical calculations is still very important despite our hi-tech environment. Good numeracy skills support the understanding of more advanced mathematical concepts at all levels. Mathematicians still consider mastery of the manual algorithms to be a necessary foundation for the study of algebra and computer science. Pupils should have a good grasp of the meaning of numbers and use their understanding of place value to multiply and divide whole numbers and fractions. They should be able to order, add and subtract negative numbers in context. They should use all four operations with decimals rounding answers where required. They should be able to solve simple problems involving ratio and direct proportion and calculate fractional or percentage parts of quantities and measurements, using a calculator where appropriate. See also the Mental Methods topic and our Number Skills Inventory.
- Decimals Working with decimals, for most pupils, presents little difficulty if the pupils have confidence working with whole numbers. The topic of decimals provides an extension to the place value system with the addition of tenths, hundredths, thousandths etc. For many pen and paper multiplication and division calculations the decimal numbers can be considered as whole numbers then the answers adjusted accordingly. So 2.4 x 2.34 can be considered as 24 x 234 ÷ 1000. The numbers are multiplied by ten and one hundred respectively then the answer needs to be divided by the ten and one hundred to compensate. Pupils should use their understanding of place value to round decimal numbers. They should also use decimal numbers in the context of measures and money. This topic also contains activities which encourage pupils to investigate and explore the properties of decimal numbers and gain a better understanding of them.
- Estimating The ability to estimate values is an often overlooked part of Mathematics. Estimating lengths, weights, time, angles and solutions to problems should be practised regularly. Pupils should make sensible estimates of a range of measures in relation to everyday situations. A basic ability to estimate quantities without counting, like when choosing a checkout line at the supermarket, can be called a person’s innate ‘number sense’. Practising this kind of estimating may actually improve a pupil’s ability in other areas of mathematics. This is one of the findings of research published in Psychological Science, a journal of the Association for Psychological Science. Practising estimation can be a lot of fun when presented as a game, challenge or group activity and provides the opportunity for the teacher to introduce variety in the mathematics classroom.
- Fractions A fraction is a part of a number. Fractions are either vulgar or decimal. Vulgar fractions can be proper, improper or mixed. Equivalent fractions have the same value. Pupils, at all stages of their learning, should practise using fractions. From dealing with halves, the most basic fraction, to manipulating algebraic fractions containing surds, this topic is always relevant. Proficiency also depends on reasonable numeracy skills particularly the multiplication tables and finding the lowest common multiple of two numbers. Pupils also need to be able to convert vulgar fractions to decimals and percentages and vice versa. Be wary of teaching the 'rules' for manipulation fractions by rote. Pupils need to understand the reason why and the time-honoured key to understanding starts with the imaginary pizza and the much-used fraction wall.
- Mental Methods Though using pencil and paper are as useful as having up-to-date technology skills, there is no substitute for strategic mental methods for working out calculations and solving problems. The activities in this topic are designed to improve pupils' abilities to use their brains. Calculating 'in your head' can be a difficult task. If you cannot remember what you have worked out or simply do not know how to solve a problem then it can be very challenging and frustrating. It is important to learn and practise mental arithmetic and using mathematical patterns, you can dramatically improve the speed and accuracy of your mental mathematics. See also the Arithmetic topic and our Number Skills Inventory.
- Negative Numbers A negative number is a real number that is less than zero. Such numbers are often used to represent the amount of a loss or absence. For example, a debt that is owed may be thought of as a negative asset, or a decrease in some quantity may be thought of as a negative increase. Negative numbers are also used to describe values on a scale that goes below zero, such as the Celsius and Fahrenheit scales for temperature. Here are some activities designed to strengthen a pupil's understanding of negative numbers.
- Rounding The objective of rounding is often to get a number that is easier to use, at the cost of making it less precise. This approximation is very important in dealing with answers to mathematical problems and making them relevant to the real world. Rounding to a given number of decimal places or significant figures is required of pupils. See also the "Approximating" Starters. Once the principles of rounding have been understood, a fun way to practise the skills is to play "Rounding Snap".
- Tables Times Tables is the common term referring to the multiples of numbers 2 to 12 (or 2 to 10). Having a quick recall of these tables is an important pre-requisite for studying other aspects of mathematics and for coping with personal finance and other area of everyday live involving numbers. People of any age can improve their skills in recalling table facts. They should learn then as they would learn a song or a dance. You need to know your times tables forwards, backwards and all mixed up. Spend time learning them well and you'll reap the benefits in future. Here on this website we have developed many activities that help pupils learn their times tables and as then revise them in different ways so that the recall becomes easier and easier. Some of the activities are games and quizzes while others help pupils spot the patterns in the times tables in many different ways. Here's a plan for learning a new times table in only five days!
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Plus Four
Work out the answers to the four given sums then add the answers together.
2nd Lesson
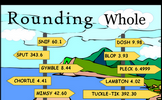
Rounding Whole
Round off the given numbers to the nearest whole number then add the answers together.
3rd Lesson
Quotients
Work out the answers to the given division calculations then add the answers together.
4th Lesson
Six Keys
Use just six calculator keys to make a total of 20. In how many different ways can it be done?
5th Lesson
Sum Story
Make up real life stories for the given calculations.
6th Lesson
Tasty Take-Aways
Four subtractions to be done without a calculator. The answers are then to be added together.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
