Simultaneous equations
Term 1 starting in week 10 :: Estimated time: 3 weeks
- Understand that equations can have more than one solution
- Determine whether a given (x, y) is a solution to a pair of linear simultaneous equations
- Solve a pair of linear simultaneous equations by substituting a known variable
- Solve a pair of linear simultaneous equations by substituting an expression
- Solve a pair of linear simultaneous equations using graphs
- Solve a pair of linear simultaneous equations by subtracting equations
- Solve a pair of linear simultaneous equations by adding equations
- Use a given equation to derive related facts (review)
- Solve a pair of linear simultaneous equations by adjusting one equation
- Solve a pair of linear simultaneous equations by adjusting both equations
- Form a pair of linear simultaneous equations from given information
- Form and solve pair of linear simultaneous equations from given information
For higher-attaining pupils:
- Determine whether a given (x, y) is a solution to both a linear and quadratic equation
- Solve a pair of simultaneous equations (one linear, one quadratic) using graphs
- Solve a pair of simultaneous equations (one linear, one quadratic) algebraically
- Solve a pair of simultaneous equations involving a third unknown
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Graph Paper Flexible graph paper which can be printed or projected onto a white board as an effective visual aid.
Deconstructing Graphs Fill in the tables of values from the information that can be read from the given graphs.
Simultaneous Shopping Find the cost of the individual items in shopping baskets (introduction to simultaneous equations).
Superfluous Find a strategy to figure out the values of the letters used in these calculations.
Simultaneous Equations Video Learn to solve simultaneous equations from the very basic to those containing quadratics. This video is to help you do the online, self-marking exercise.
Simultaneous Equations A self-marking, multi-level set of exercises on solving pairs of simultaneous equations.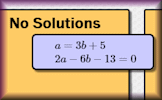
Simultaneous Solutions Arrange the given pairs of simultaneous equations in groups to show whether they have no solution, one solution or infinite solutions.
Unbeknownst Some picture grid puzzles which can be solved by using simultaneous equations.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.
Here are some exam-style questions on this topic:
- "Nora and Dora are trying to solve the following simultaneous equations by finding the intersection of their graphs." ... more
- "(a) Use the red graphs to solve the simultaneous equations:" ... more
- "Solve the simultaneous equations" ... more
- "Estimate the solutions of the following simultaneous equations using their graphs as drawn on the grid below." ... more
- "Solve the simultaneous equations:" ... more
- "A rectangular sheet of paper can be cut into two identical rectangular pieces in two different ways, either by cutting along line A or by cutting along line B." ... more
- "Show that you understand equations and inequalities by answering the following:" ... more
- "Draw the graph of \(y = 2x^2 + 3x - 7\) for \( -3.5 \le x \le 2\). Draw suitable straight lines to find approximate solutions (to one decimal place) of the equations:" ... more
- "Solve algebraically the simultaneous equations to find the solution where \(-10 \le x \le 10\)." ... more
- "Two numbers are chosen so that the sum of their squares is 25." ... more
- "The prices of two watches are in the ratio \(a:b\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Coordinates It is important that pupils become proficient at understanding coordinates at a basic level before using them in their study of graphs. Plotting points and finding the coordinates of points are the pre-requisite skills for studying a number of branches of mathematics. The Cartesian plane consists of a horizontal x-axis and a vertical y-axis that intersect at the origin (0, 0). The mathematician René Descartes developed the concept of the Cartesian plane while lying in bed one morning and observing a fly on the ceiling! Pupils should learn the conventions starting with knowing that the horizontal axis is the x-axis and the vertical axis is the y-axis (remember x is a cross so the x axis is across!). The axes meet at the origin which has coordinates (0,0). Coordinates are written as two numbers separated by a comma and contained inside brackets. For example (3,9) means the point is above 3 on the x-axis and level with 9 on the y-axis. To get to this point from origin you go along 3 and up 9 (remember to go along the hall before going up the stairs or that pole vaulter has to run along before leaping up into the air!). Coordinates can be positive or negative (remember points to the right of the origin have a positive x-coordinate – being positive is right!). The abscissa often refers to the horizontal coordinate of a point and the ordinate refers to the vertical coordinate. In three dimensions, three perpendicular lines are defined as the axes and the coordinates of each point is defined with three numbers.
- Simultaneous Equations This topic covers simultaneous equations with two different variables. The starters pose real world problems which can be solved using the techniques taught at school or by other intuitive methods. Though there are many formal strategies for solving simultaneous equations the skill of forming the equations from real life situations is a very important stage in working towards a solution. Algebraic methods are the most efficient for solving basic simultaneous equations but graphical methods, probably using a graphic display calculator or computer software package, may be more suitable for less standard sets of simultaneous equations.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Oblongs
Find the dimensions of a rectangle given the perimeter and area.
2nd Lesson
Rabbits and Chickens
There are some rabbits and chickens in a field. Calculate how many of each given the number of heads and feet.
3rd Lesson
Rail Weigh
Use the weights of the trains to work out the weight of a locomotive and a coach. A real situation which produces simultaneous equations.
4th Lesson
Simultaneous Occasions
A problem which can best be solved as a pair of simultaneous equations.
5th Lesson
Summer Holidays
How many children and how many donkeys are on the beach? You can work it out from the number of heads and the number of feet!
6th Lesson
Two Numbers
Find the two numbers whose sum and product are given.
7th Lesson
Same Same
A problem involving two people's ages which can be solved using algebra.
8th Lesson
Planet Numpair
The sum and product are given, can you find the two numbers?
9th Lesson
Santa's Sleigh
Work out the number of clowns and horses given the number of heads and feet.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
