
 |
Exam-Style Questions on TrigonometryProblems on Trigonometry adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
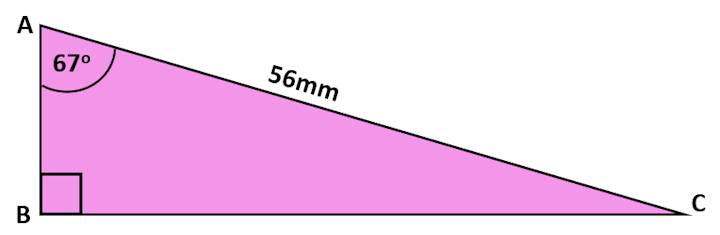
The diagram (not drawn to scale) shows a right-angled triangle.
Calculate the length of side BC to three significant figures.
2. | GCSE Higher |
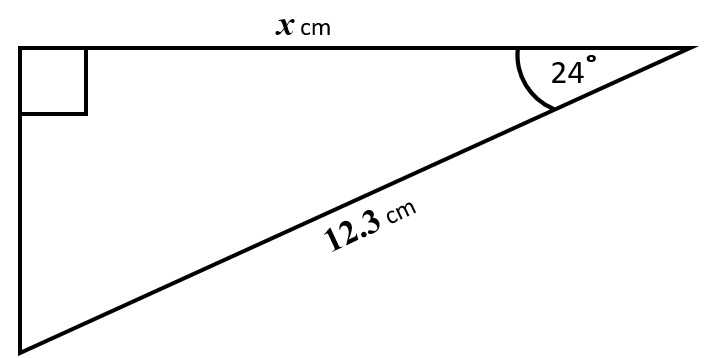
Work out the value of \(x\), the length in centimetres of one of the sides of this right-angled triangle.
Give your answer correct to 1 decimal place.
3. | GCSE Higher |
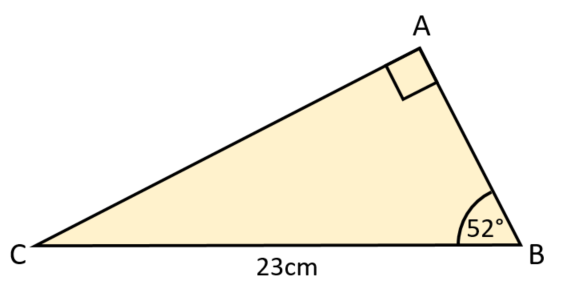
ABC is a right-angled triangle as shown in the diagram below. Calculate the length of AB giving your answer correct to three significant figures.
4. | GCSE Higher |
An arborist sights the top of a tree using a clinometer and reads the angle of elevation to be 29o. Her clinometer is 28 metres from the base of the tree and is on a tripod making it 1.5 metres above ground level.
This diagram is not drawn to scale.
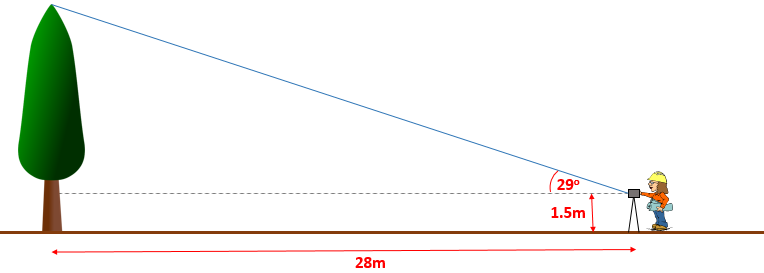
Calculate the full height of the tree.
5. | GCSE Higher |
Here is triangle PQR:
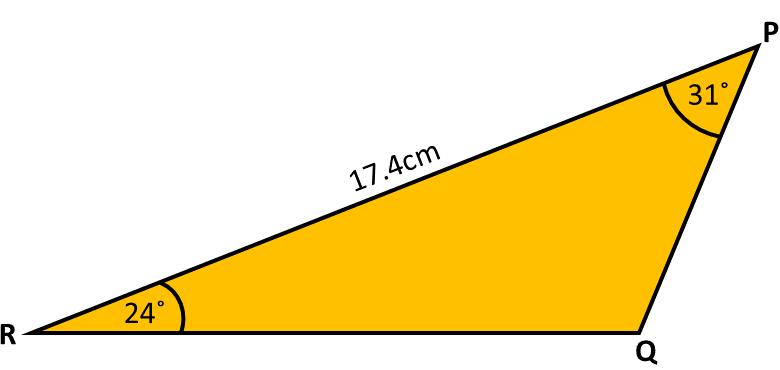
Work out the length of PQ.
Give your answer correct to 1 decimal place.
6. | GCSE Higher |
The diagram shows a trapezium where the sides AC and BD are parallel.
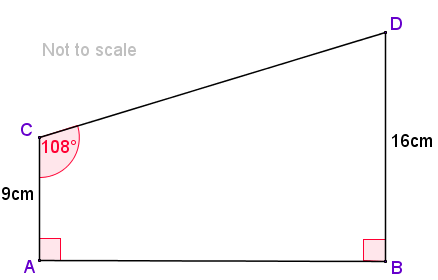
Calculate the length of side CD
7. | GCSE Higher |
The area of the triangle is 10.6 cm2. Calculate the value of \(\sin {x}\).
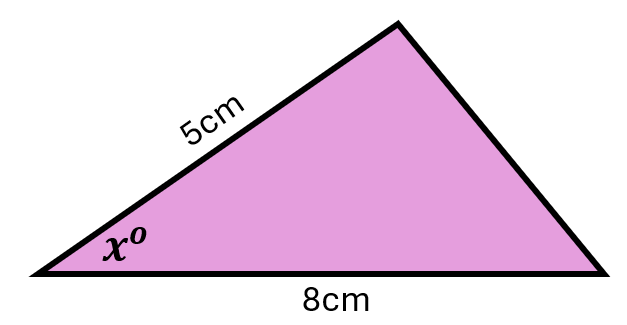
8. | GCSE Higher |
Taptaya Park Tower is over two hundred metres tall. There is a zip wire from the observation deck to a point on the ground 550 metres away in a northerly direction.

(a) If the beginning of the zip wire is 210 metres above the ground find the angle of depression of the end point of the zip wire as seen from the beginning.
It is decided that the zip wire is slightly too steep so the end point is moved so that it is now further away.
(b) Find the horizontal distance if the angle of elevation of the beginning of the zip wire as seen from the end is now 18o.
9. | GCSE Higher |
Triangle ABC has a right angle at C.
Angle BAC = 54°.
AB = 22.6 cm.
Calculate the length of BC to three significant figures.
10. | IB Studies |
Neung is at Bangkok's Suvarnabhumi Airport watching the planes take off. He observes a plane that is at an angle of elevation of 25o from where he is standing at point N. The plane is at a height of 390 metres as can be seen in the following diagram (not to scale).
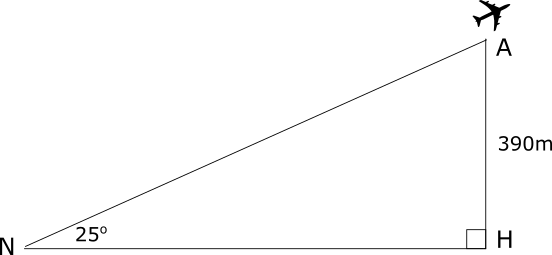
(a) Calculate the horizontal distance, NH, of the plane from Neung. Give your answer to the nearest metre.
The plane took off from a point T, which is 230 metres from where Neung is standing, as shown in the following diagram (not to scale).

(b) Calculate the angle ATH, the take-off angle of the plane to the nearest degree.
11. | GCSE Higher |
Find the exact value of tan45° × sin30° × cos30°
Give your answer in its simplest form.
12. | GCSE Higher |
The diagram shows a quadrilateral, ABCD, formed from two triangles, ABC and ACD.
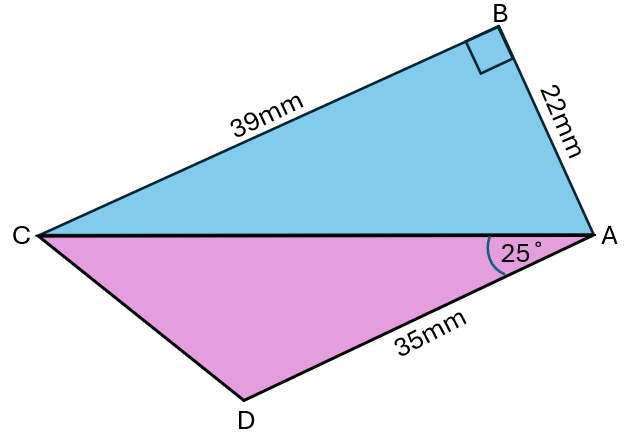
ABC is a right-angled triangle.
(a) Calculate angle BAC.
(b) Calculate BD.
(c) Calculate the shortest distance from D to AC.
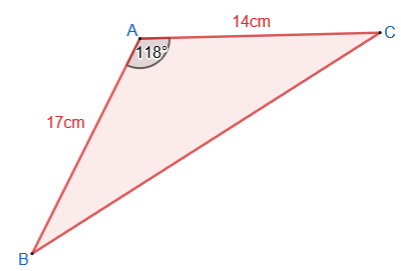
13. | GCSE Higher |
Consider the triangle ABC where AB=17cm, AC=14cm and the angle BAC = 118o. Find the length of BC.
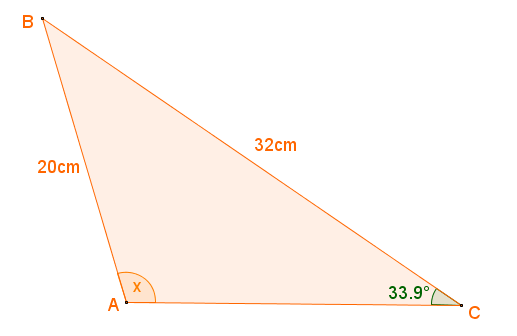
14. | GCSE Higher |
The angle marked \(x\) in the diagram below is obtuse. Find the value of \(x\)
15. | IB Studies |
The Tamarack triathlon race consists of swimming, cycling and running. Competitors swim from A to B, then cycle from B to C and finally run from C back to A.
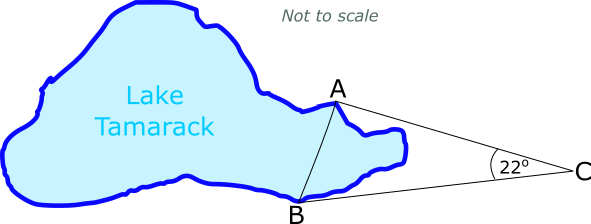
Angle ACB is 22o.
It takes Walter 10 minutes and 20 seconds to cycle from B to C at a speed of 29kmh-1.
(a) Find the distance from B to C in kilometres.
The distance from C to A is 4 kilometres. Running this part of the course takes Walter 25 minutes.
(b) Calculate the speed, in kilometres per hour, that Walter runs from C to A.
(c) Calculate the distance, in kilometres, from A to B.
(d) Calculate the total distance, in kilometres, of the triathlon course.
(e) Find the size of angle ABC.
(f) Calculate the area of the triathlon course bounded by the lines AB, BC and CA.
16. | GCSE Higher |
(a) Write down the exact value of \(\tan 60^o\).
(b) Find the exact area of this triangle.

17. | GCSE Higher |
Rectangle ABCD is the horizontal base of a trapezoidal prism ABCDEFGH.
EF is parallel to AB. BC = 20cm, DC = 150mm, GC = 74mm, HG = 86mm and AE = BF.
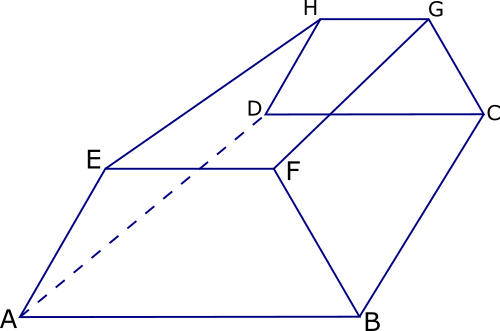
(a) Find the size of angle ABF.
(b) Show that FD = 242 mm correct to 3 significant figures.
18. | GCSE Higher |
A triangular prism is made using two right-angled triangles and three rectangular pieces of cardboard. Five of the vertices have been labeled \(A, B, C, D \text{ and } E\) as shown in the photograph below.

$$ AB = 17cm, \quad BC = 24cm, \quad DC = 28cm $$
Imagine a point \(F\) on the line \(DC\) such that:
$$ DF : FC = 3 : 4 $$Calculate the size of the angle between \(AF\) and the base of the prism.
19. | GCSE Higher |
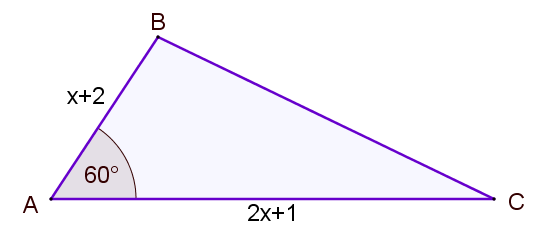
The area of triangle ABC (not drawn to scale) is
$$ \frac{35 \sqrt{3}}{4} m^2$$If AB = \(x+2\) metres and AC = \(2x+1 \) metres, find the value of \(x\).
20. | GCSE Higher |
The diagram shows parallelogram ABCD in which AD = \(x\) cm, DE = 12 cm and angle ABC = 30°
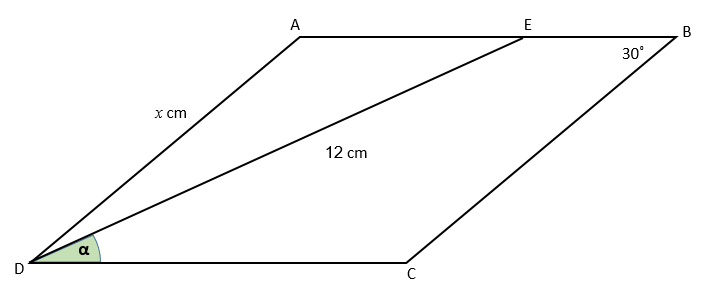
Prove that α, the size of angle CDE, is sin-1\( \left( \frac{x}{24} \right) \)
21. | IB Standard |
In triangle ABC, AB = 7cm and AC = 9cm. The area of the triangle is 20cm2.
(a) Find the two possible values for the angle A.
(b) Given that A is obtuse, find the length of the side BC.
22. | IB Studies |
ABC is a triangular car park on horizontal ground. The length of AB is 90m and the length of AC is 65m. The size of angle BCA is 68o.
(a) Find the size of angle ABC.
(b) Find the area of the triangular car park.
M is the midpoint of AC.
(c) Find the length of BM.
A vertical flag pole, FB, is erected in one corner of the car park with its base at B.

The angle of elevation of F from M is 55.3o. H is the midpoint of the flag pole.
(d) Calculate the angle of elevation of H from M.
23. | IGCSE Extended |
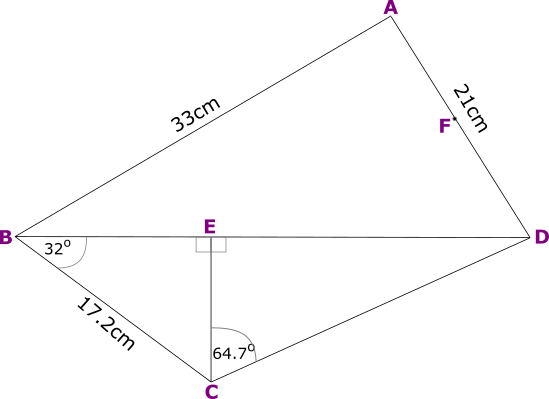
The diagram (not to scale) shows a quadrilateral made up of a number of triangles.
The area of triangle ABD is 333 cm2 and AD = 21 cm and AB = 33cm.
(a) Calculate the size of acute angle DAB.
(b) The midpoint of AD is F. Use the cosine rule to calculate the length of BF.
(c) Calculate the length of CD.
(d) \(\sin x = \cos 38^o, 0^o \le x \le 180^o\), Find the two values of \(x\).
25. | GCSE Higher |
The diagram shows quadrilateral \(ABCD\) and is not drawn to scale.
(a) Calculate angle \(CBD\)
(b) Find the length of \(AB\) correct to 2 decimal places.
(c) Calculate the shortest distance from \(A\) to \(BD\).
(d) Calculate the length of the straight line \(AC\).
(e) \(B\) is due west of \(D\). Find the bearing of \(C\) from \(D\).
26. | GCSE Higher |
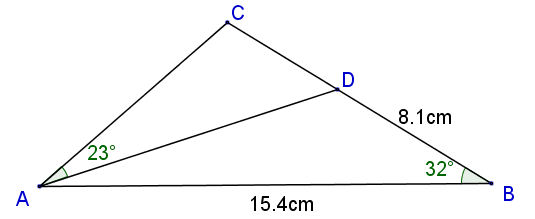
In the diagram of triangle ABC (not to scale) D is a point on BC.
AB = 15.4cm, BD = 8.1cm, angle CAD = 23o and angle ABD = 32o.
Calculate the area of triangle ADC.
27. | IB Standard |
The diagram, not drawn to scale, shows a quadrilateral ABCD.
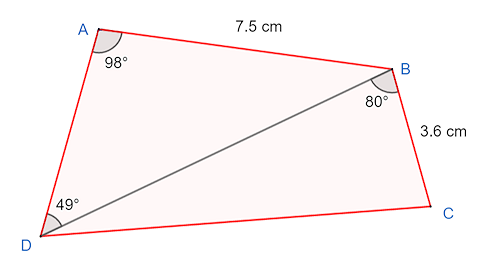
AB = 7.5cm, BC = 3.6cm, angle DAB = 98o, angle DBA = 49o and angle DBC = 80o
(a) Find DB
(b) Find DC
(c) The area of triangle ABD
28. | IB Analysis and Approaches |
In triangle ABC, the length of AB = 5cm, AC = 13cm and \( \cos B \hat AC = \frac18 \).
(a) find the value of \( \sin B \hat AC \)
(b) Find the area of triangle ABC.
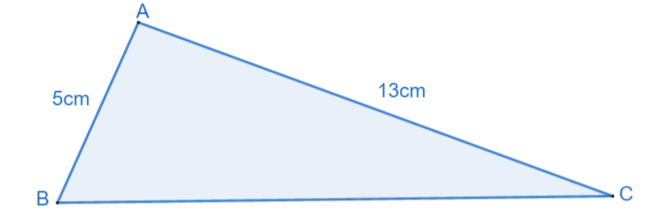
Diagram not to scale
29. | IB Analysis and Approaches |
An astronaut measures the angle of elevation of a light on the surface of a mysterious sphere on a faraway planet.
The light is level with the centre of the sphere, so its distance above the ground is equal to the radius of the sphere.
The astronaut measures the angle to be 20°, and his theodolite is 15 metres away from the centre point where the sphere touches the ground. The theodolite is 1.7 metres tall.

(a) Calculate the radius of the sphere.
(b) Calculate the volume of the sphere.
30. | IB Standard |
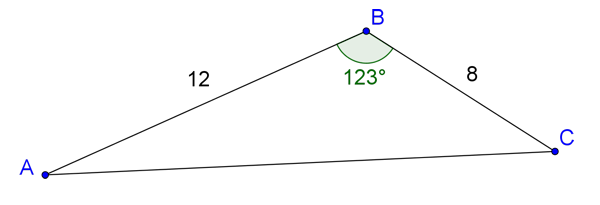
In the diagram above (not drawn to scale), AB=12mm, BC=8mm and angle ABC=123o
(a) Find the length of side AC.
(b) Find angle BAC.
31. | IB Analysis and Approaches |
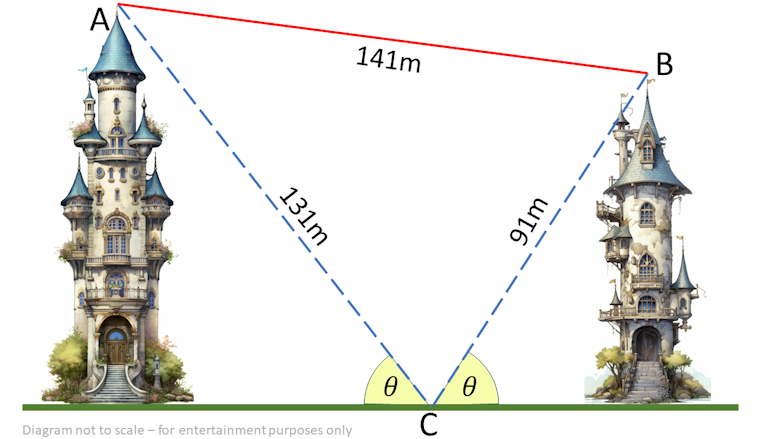
Two towers are situated close to each other on level ground. From point C on the ground directly between the two buildings, the angle of elevation to the top of each tower is \( \theta \).
The distance from point C to point A at the top of the taller building is 131 metres.
The distance from point C to point B at the top of the shorter building is 91 metres.
The distance between A and B is 141 metres.
Find the heights of the two towers to the nearest metre.
32. | IB Analysis and Approaches |
The diagram below shows triangle ABC and the lengths of its sides. It is known that the cosine of angle \(C\hat{A}B\) is one third.
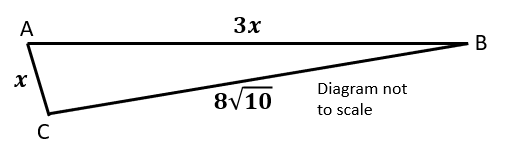
Find the area of the triangle giving your answer in the form:
$$ m \sqrt{n} \text{ where } m, n \in \mathbb{Z}^+ $$33. | IB Analysis and Approaches |
Consider a triangle DEF, where DF= 15cm, FE = 9cm and EDF = 21°.
Find the largest possible perimeter of triangle DEF.
34. | IB Standard |
The diagram shows quadrilateral ABCD.
(a) Use the cosine rule to show that \(AC = \sqrt{130-126\cos{A\hat{B}C}}\).
(b) Use the sine rule in triangle \(ABC\) to find another way of writing \(AC\).
(c) Hence find the value of \(A\hat{B}C\), assuming it is an obtuse angle, giving your answer to two the nearest degree.
(d) Find \(AC\) to three significant figures.
(e) Find \(C\hat{D}A\) to three significant figures.
(f) Hence, or otherwise, find the area of triangle \(ACD\).
35. | IB Studies |
Christine owns a four sided piece of land shown in the diagram below as ABCD. The length of BC is 180 m, the length of CD is 70 m, the length of AD is 90 m, the size of angle BCD is 82° and the size of angle BAD is 102°. The diagram is not to scale
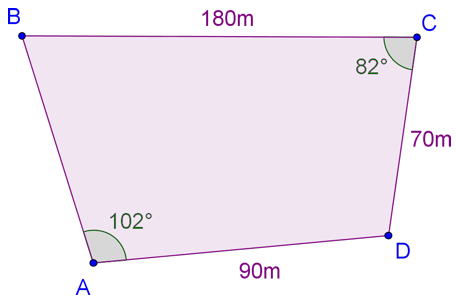
Christine decides to sell the triangular portion of land ABD. She first builds a straight fence from B to D.
(a) Calculate the length of the fence.
The fence costs 19 USD per metre to build.
(b) Calculate the cost of building the fence. Give your answer correct to the nearest USD.
(c) Show that the size of angle ABD is 28.6°, correct to three significant figures.
(d) Calculate the area of triangle ABD.
She sells the land for 110 USD per square metre.
(e) Calculate the value of the land that Christine sells. Give your answer correct to the nearest USD.
Christine invests 200 000 USD from the sale of the land in a bank that pays compound interest compounded annually.
(f) Find the interest rate that the bank pays so that the investment will double in value in 12 years.
36. | IB Studies |
A builder marks out three points A, B and C on the ground such that AB = 11m , AC = 15m and angle BAC = 124o.
(a) Calculate the length of BC.
He next marks a fourth point, D, on the ground at a distance of 12m from B, such that angle BDC is 53o.
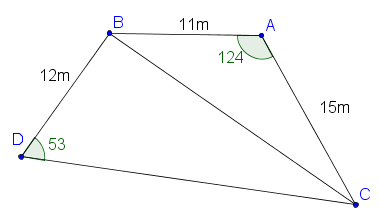
(b) Find the size of angle DBC.
(c) Find the area of the quadrilateral ABDC.
The builder digs up and removes the soil under the quadrilateral ABDC to a depth of 90 cm for the foundation of the house.
(d) Find the volume of the soil removed. Give your answer in m3
To transport the soil removed, the builder uses cylindrical drums with a diameter of 46cm and a height of 70cm.
(e) Find the volume of a drum. Give your answer in m3.
(f) Find the minimum number of drums required to transport the soil removed.
37. | IB Applications and Interpretation |
Melissa has a webcam on the top of her computer screen. She has the zoom level adjusted so that that her head is framed nicely in the image produced. The diagram shows the setup.
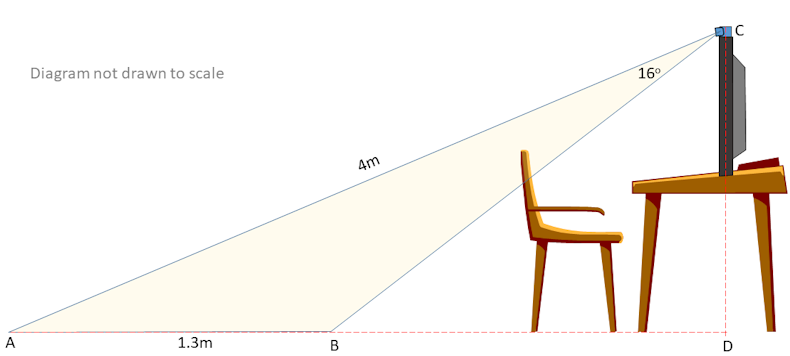
The webcam is at point C directly above point D on the floor. The area covered by the camera is shown by the shaded region enclosed by triangle ABC. The distance from A to C is 4 m and the distance from A to B is 1.3 m. Angle ACB is 16o.
(a) Find angle ABC.
Melissa's younger brother is 95cm tall. He walks into the room from the door at the opposite end of the room from Melissa's computer. When he reaches point A his feet first appear in the video being recorded by the webcam. He continues to walk until the top of his head is in shot at which points he stops.
(b) How far is Melissa's brother from point A?
38. | IB Studies |
A drone flying test course is in the shape of a triangle, ABC, with AB = 400m , BC = 600m and angle ABC = 44o. The course starts and finishes at point A.
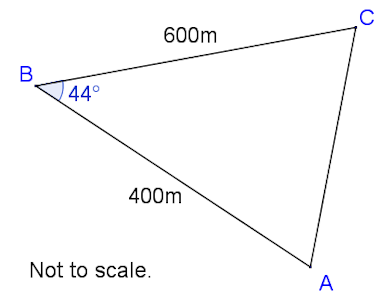
(a) Calculate the total length of the course to the nearest metre.
It is estimated that a drone can travel at an average speed of 4.5ms–1.
(b) Calculate an estimate of the time taken to fly around the course. Give your answer to the nearest minute.
(c) Find the size of angle ACB.
To comply with safety regulations, the area inside the triangular course must be kept clear of people, and the shortest distance from B to AC must be greater than 275 metres.
(d) Calculate the area that must be kept clear of people.
(e) Determine, giving a reason, whether the course complies with the safety regulations.
The course is viewed from a tower which rises vertically from point A. The top of the tower is point T. The angle of elevation of T from B is 8o.
(f) Calculate the vertical height, AT , of the tower.
39. | IB Standard |
The diagram shows a circle of radius 8.6cm with points ABCD on the circumference of the circle.
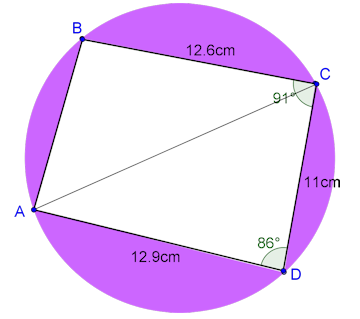
(a) Find the length of line AC.
(b) Find angle ACD.
(c) Use your answer to part b to find angle ACB.
(d) Find the area of triangle ADC.
(e) Find the total area of the shaded regions.
40. | A-Level |
The cosine of acute angle \( \alpha \) is \( \frac{1}{ \sqrt 5} \)
The angle \( \beta \) is obtuse and \( \sin \beta = \sqrt \frac{2}{3} \).
(a) Find exact values of \( \tan \alpha \) and \( \tan \beta \).
(b) Hence show that \( \tan( \alpha - \beta ) \) can be written as \(a+b \sqrt 2 \) where \(a\) and \(b\) are rational numbers41. | IB Analysis and Approaches |
Emma sails in a small dinghy from point A in a straight line to a buoy at point B. She is moving at an average speed of 19 km/h, for 6 minutes, on a bearing of 125°.
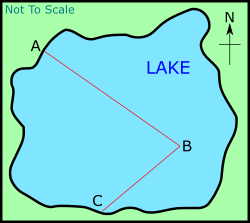
(a) Find the distance from point A to point B
(b) When Emma arrives at point B she changes direction and sails to point C on a bearing of 230° and 1 km away. Find angle ABC
(c) Find the distance from point A to point C.
(d) Find angle BCA
(e) Emma’s friend Eamonn wants to swim directly from point A to point C. Find the bearing that Eamonn must take to point C.
(f) Eamonn swims at an average speed of 3.2 km/h. Find, to the nearest minute, the time it takes for Eamonn to reach point C.
42. | IB Standard |
The diagram shown the origin O (0,0) and a fixed point A(10,2). The point P moves along the horizontal line \(y = 8\).
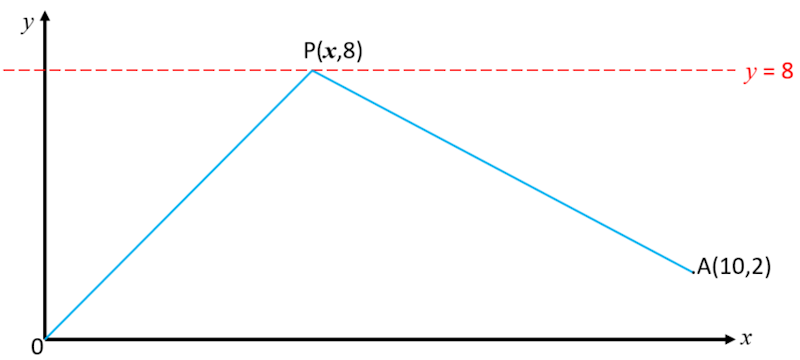
(a) Show that \(PA = \sqrt{x^2 - 20x + 136} \)
(b) Write down a similar expression for \(OP\) in terms of \(x\)
(c) Hence, show that:
$$ \cos O\hat{P}A = \frac{x^2-10x+48}{\sqrt{(x^2 + 64)(x^2 -20x +136)}} $$Let this expression for the cosine of \( O\hat{P}A \) be defined as function \(f\).
(d) Find the size of angle \( O\hat{P}A \) in degrees when \(x=5\).
(e) Find two positive values of \(x\) such that \( O\hat{P}A = 60^o\).
(f) Consider the equation \( f(x) = 1 \). Explain, in terms of the positions of the points O, A and P, why this equation has a solution.
(g) Find the exact solution of \( f(x) = 1 \).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.