
 |
Exam-Style Questions on ProbabilityProblems on Probability adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
There are only crayons in a pencil case and the crayons are either orange, purple or brown.
The table shows the probability of taking at random a brown crayon from the pencil case.
| Colour: | orange | purple | brown |
|---|---|---|---|
| Probability: | 0.4 |
The number of orange crayons in the pencil case is the same as the number of purple crayons.
(a) Complete the table.
There are 20 brown crayons in the pencil case.
(b) Work out the total number of crayons in the pencil case.
2. | GCSE Higher |
The following table shows the probabilities of winning certain prizes at a stall in Faulton Towers theme park. A prize is always given for every turn.
| Prize | Pencil | Calculator | Teddy Bear | Ball | Protractor |
|---|---|---|---|---|---|
| Probability | 0.65 | 0.02 | 0.05 | 0.26 | ? |
In the last year Simon has had 200 turns receiving 200 prizes.
Work out an estimate for the total number of times he has won either a pencil or a protractor.
3. | GCSE Higher |
Derren thinks he is a mind reader and can tell what Paige is thinking. An experiment was conducted to test this.
Derren and Paige sit either side of a screen and Paige rolls a six-sided fair dice. Paige then thinks about the number on the dice while Derren tries to predict this number.
(a) In 900 attempts, how many correct predictions would you expect Derren to make if he was just guessing?
The results of the first 15 attempts are shown in the table:
| Paige's Number | 4 | 6 | 3 | 3 | 3 | 2 | 2 | 2 | 3 | 1 | 1 | 5 | 1 | 1 | 2 |
| Derren's Guess | 1 | 2 | 2 | 4 | 2 | 2 | 1 | 4 | 2 | 4 | 2 | 6 | 1 | 2 | 2 |
| Guess Correct | ✓ | ✓ | ✓ |
(b) Estimate the probability of getting a matching pair using the results of the last five guesses.
(c) Estimate the probability of getting a matching pair using all 15 results.
(d) Use this information to comment on Derren’s belief that he knows what Paige is thinking.
4. | GCSE Higher |
The midnight train to Georgia is not the most reliable. The probability that the train will be late on any day is 0.35
(a) Complete the probability tree diagram for Monday and Tuesday.
Monday Tuesday
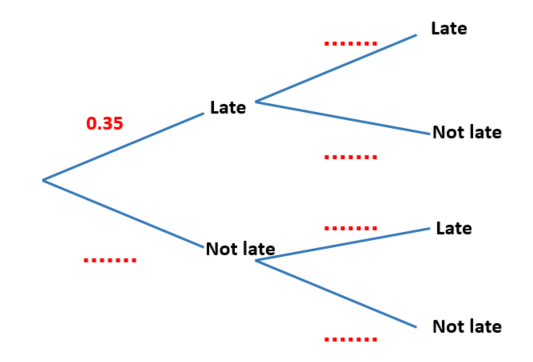
(b) Work out the probability that the train will be late on at least one of these two days.
5. | GCSE Higher |
At the Trantown annual Fayre there are a number of different sideshows designed to raise money for cancer research. Roger is looking after two of these, the lucky dip and the raffle.
(a) At the lucky dip it costs £1 to enter and everyone wins one of three different types of prize.
Calculate the value of \(x\).

(b) Roger is offering a free raffle ticket for every raffle ticket purchased. He tells people that this doubles their chances of winning. Is he correct?
6. | GCSE Higher |
The table shows the shoe sizes of 35 male teachers.
| Shoe size | Number of teachers |
|---|---|
| 7 | 4 |
| 8 | 6 |
| 9 | 10 |
| 10 | 12 |
| 11 | 3 |
Eight of the 35 teachers do not wear socks.
Ralph thinks that if you choose at random one of the 35 teachers, the probability that he either does not wear socks or wears the median shoe size is \( \frac{17}{35} \) because:
$$ \frac{8}{35} + \frac{9}{35} = \frac{17}{35} $$Is Ralph correct? Give a reason for your answer.
7. | GCSE Higher |
Carol has two fair 5-sided spinners. One spinner is pink and the other is green.
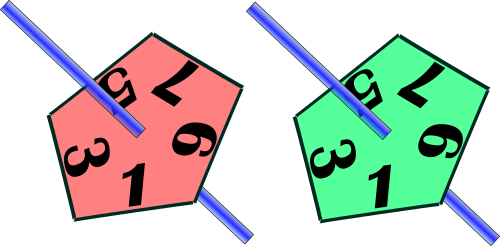
The spinners could land on any of the single digit odd numbers with equal probability.
(a) Draw a tree diagram to show the probabilities of either, or both spinners landing on a square number.
(b) Work out the probability that the pink spinner lands on a square number and the green spinner does not.
8. | GCSE Higher |
The diagram shows 13 fruit emojis.
🍊 🍎 🍌 🍎 🍊 🍎 🍋 🍎 🍎 🍌 🍒 🍒 🍒
(a) One of the emojis is chosen at random. Write down the probability that it is not an apple.
(b) An emoji is chosen at random from these 13 emojis and then replaced. A second emoji is then chosen at random. Find the probability that exactly one emojis is a banana.
9. | GCSE Higher |
(a) There are 24 people at a Football Club supporters' meeting in Dudley. Thirteen of them are female.
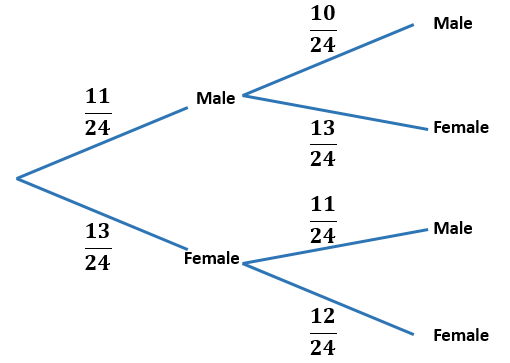
First chosen Second chosen
Tracey draws the tree diagram above to show how two people could be chosen from the meeting at random. What is wrong with the probabilities shown on the diagram?
(b) Aynuk and Ayli play for Dudley Casuals Football Club. The probabilities that they will score a goal in the next match are 0.2 and 0.35 respectively.
The manager thinks that the probability that both players will score a goal in the next match is 0.2 + 0.35. Is the manager correct? Give reasons for your answer.
10. | GCSE Higher |
Mrs Gill wants to give her nephew two sweets from a jar she keeps on her kitchen table. There are 11 sweets in this jar.
Calculate the probability that Mrs Gill will take a sweet of each colour if she takes two sweets randomly from the jar.
Show all of your working.
11. | GCSE Higher |
Aran, Betsy and Connor collect data about which way up a drawing pin will land if dropped from a fixed height. Here are their results.
| Pin up | Pin down | Total | |
| Aran | 24 | 33 | 57 |
| Betsy | 22 | 33 | 55 |
| Connor | 86 | 102 | 188 |
Aran thinks "As a drawing pin can only land with its pin up or with its pin down so the probability of a drawing pin landing pin up is 0.5"
(a) Explain whether you agree or disagree with his statement and give a reason.
(b) Connor's results give the best estimate of the probability of a pin landing pin up. Explain why.
(c) Two pins are dropped. Estimate the probability that both pins land pin down.
12. | GCSE Higher |
During a demonstration for Year 10 pupils a biased coin in a computer simulation landed on heads 600 times.
The relative frequency of heads was 0.3
Work out the number of times the coin landed on tails during that demonstration.
13. | GCSE Higher |
There are 1200 pupils at Thailand's largest British International school. 690 of these pupils are girls.
The probability that a boy chosen at random buys lunch from the school canteen is \( \frac{4}{5} \).
The probability that a girl chosen at random buys lunch from the school canteen is \( \frac{2}{3} \).
(a) Work out the number of students in the school who buy lunch from the school canteen.
(b) Work out the probability that a student chosen at random from the whole school does not buy lunch from the school canteen.
14. | IGCSE Extended |
For this question, give all your answers as fractions.
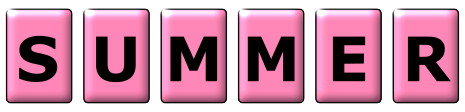
The letters of the word SUMMER are printed on 6 cards.
(a) A card is chosen at random. Write down the probability that it has the letter R printed on it.
(b) Find the probability that the card chosen at random does not have the letter M printed on it.
(c) Find the probability that the letter printed on the card chosen at random has no lines of symmetry.
(d) Chris chooses a card at random, replaces it, then chooses a card again. Calculate the probability that only one of the cards she chooses has the letter M printed on it.
(e) Graham chooses a card at random and does not replace it. He continues until he chooses a card with the letter M printed on it. Find the probability that this happens when he chooses the 3rd card.
15. | GCSE Higher |
There are some discarded marker pens in a bin.
The pens are blue or green or red or yellow.
The table shows the probabilities that a pen taken at random from the bin will be red or yellow.
| Colour | Blue | Green | Red | Yellow |
| Probability | 0.44 | 0.12 |
The probability that a pen taken at random from the bin will be blue is three times the probability that the pen will be green.
There are 500 pens in the bin.
Work out the number of green pens in the bin.

16. | GCSE Higher |
The Venn diagram represents a collection of 40 books on sale in an online store.
P represents the books available in paperback format.
D represents the books available in digital format.
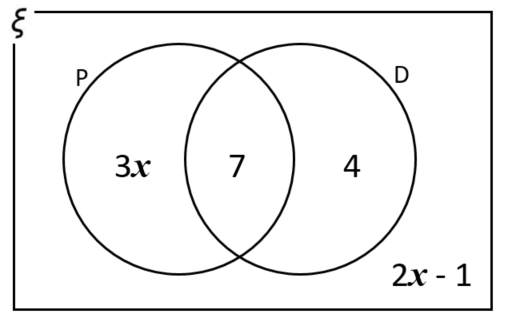
(a) One book from the collection is picked at random. Work out the probability that the book is available in digital format.
(b) One of the books that is available in paperback format is picked at random. Work out the probability that this book is also available in digital format.
17. | GCSE Higher |
A box contains only green and yellow crayons.
Luka takes one crayon at random from the box. The probability that she takes a green crayon is \(\frac16\).
Luka returns the crayon to the bag and adds four more green crayons to the box. The probability that she takes one green crayon at random is now \(\frac14\).
How many crayons of each colour were originally in the box?
18. | GCSE Higher |
At an international conference there were 300 delegates from both the northern and southern hemispheres. Each delegate wore a t-shirt in one of three different colours:
The table gives some information about the delegates.
| T-shirt colour | Total | |||
|---|---|---|---|---|
| Red | Blue | Green | ||
| Northern | 76 | 190 | ||
| Southern | 36 | 25 | 110 | |
| Total | 105 | 101 | 300 | |
(a) Complete the table.
(b) Find the probability that one of these delegates chosen at random wears a red t-shirt.
(c) Two of these delegates are chosen at random.
Find the probability that they are both from the southern hemisphere.
(d) Two of the delegates from the southern hemisphere are chosen at random.
Find the probability that they both were born after 2012.
(e) Two of the Generation Z delegates are chosen at random.
Find the probability that one is from the northern hemisphere and the other is from the southern hemisphere.
19. | GCSE Higher |
Lisa's nephew Sean has two boxes containing plastic building bricks.
A red box contains 5 green bricks and 10 yellow bricks.
A blue box contains 8 green bricks and 16 yellow bricks.
Lisa picks a brick at random from the red box and puts it into the blue box.
Sean now picks a brick at random from the blue box. Show that:
P(Lisa picks a green brick) = P(Sean picks a green brick)
20. | GCSE Higher |
80 students are asked if they like History (\(H\)) and if they like Geography (\(G\)).

7 say they do not like History and do not like Geography.
45 say they like History.
54 say they like Geography.
(a) Draw a Venn diagram to represent this situation.
A student is chosen at random.
(b) Find the probability that this student likes History and likes Geography.
Two students are chosen at random.
(c) Find the probability that they both like Geography.
Two students who like History are chosen at random.
(d) Find the probability that they both also like Geography.
21. | IB Studies |
Neal is attending a Scout jamboree in Japan. He has both boots and trainers to wear. He also has the choice of wearing a cap or not.
The probability Neal wears boots is 0.4. If he wears boots, the probability that he wears a cap is 0.7.
If Neal wears trainers, the probability that he wears a cap is 0.25.
The following tree diagram shows the probabilities for Neal's clothing options at the jamboree.
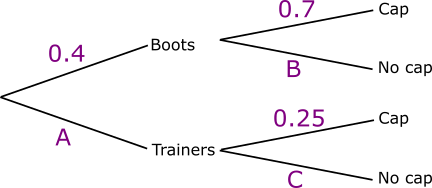
(a) Find the value of A.
(b) Find the value of B.
(c) Find the value of C.
(d) Calculate the probability that Neal wears trainers and no cap.
(e) Calculate the probability that Neal wears no cap.
(f) Calculate the probability that Neal wears trainers given that he is not wearing a cap.
(g) Calculate the probability that Neal wears boots on the first two days of the jamboree.
(h) Calculate the probability that Neal wears boots on one of the first two days, and trainers on the other.
22. | GCSE Higher |
A monkey comes across a box of red and green apples in the jungle. All of the apples are the same size.

There are \(n\) red apples in the box.
There are 9 green apples in the box.
The monkey is going to take at random an apple from the box.
The primatologist who provided the box of apples and who is observing the monkey's behaviour suspects the monkey is colour blind. He concludes that the probability that the apple will be red is \( \dfrac{3}{7} \).
(a) Show why the probability cannot be \( \dfrac{3}{7} \).
After the monkey has taken the first apple from the box and eaten it, he is going to take at random a second apple from the box.
(b) Given that the probability that both the apples he takes will be red is \( \dfrac{2}{5} \) work out the number of red apples in the box.
You must show all your working.
23. | GCSE Higher |
Percy throws a fair dice until he gets a five.
(a) Work out the probability that Percy gets the five on his first throw.
(b) Find the probability that he has to throw the dice exactly twice to get the five.
(c) Calculate the probability that he will have the throw the dice more than twice to get a five.
24. | GCSE Higher |
Donna is in a class of 25 students, 5 of whom have a pet dog.
There are 2200 students in the school.
(a) Use this information to estimate how many students in the school have pet dogs.

(b) Luka is at a different school.
She is in a class of 28 students, 7 of whom have pet dogs.
Luka and Donna have an idea. They think "In our two classes there are 53 students, 12 of whom have a pet dog. We can use this bigger sample to improve the estimate for Donna's school."
What assumption have they made?
(c) Use this idea to estimate how many students in Donna's school have pet dogs.
25. | IB Standard |
Let \(J\) and \(T\) be independent events, where \(P(J)=0.4\) and \(P(T)=0.7\).
(a) Find \(P(J\cap T)\).
(b) Find \(P(J\cup T)\).
(c) Draw a two-set Venn diagram and shade the region that represents \(J\cap T'\).
(d) Find \(P(J\cap T')\).
26. | GCSE Higher |

On the day after one GCSE paper Twitter and the media were buzzing with comments about a particular question about Hannah's sweets. Here is the Transum version of this now famous Maths exam question:
Hannah has 6 orange sweets and some yellow sweets.
Overall, she has \(n\) sweets.
The probability of her taking 2 orange sweets is \(\frac13\).
Prove that: \(n^2-n-90=0\)
Hence or otherwise find \(n\).
27. | GCSE Higher |
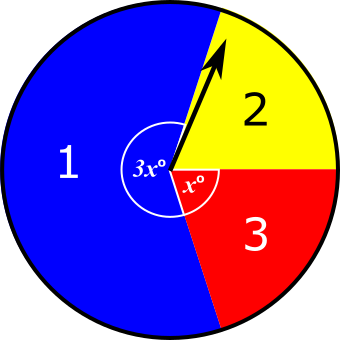
When the arrow is spun once on this spinner, a 1 or a 2 or a 3 can be scored depending on the colour the arrow lands on.
Aimee is going to spin the arrow twice. She will work out her total score by adding the two scores she gets on the two spins. The probability that she will get a total score of 4 is \(\frac{7}{25}\)
Find the value of \(x\).
28. | GCSE Higher |
A bag contains balls that are red, blue, green or yellow.
A counter is chosen at random. The probability it is green is \( \frac{7}{52} \)
Work out the probability it is red.
29. | GCSE Higher |
There are \(x\) left shoes and 7 right shoes in a dark cupboard.
Harper takes at random two shoes from the cupboard.
The probability that Harper takes one left shoe and one right shoe is \(\frac{7}{13}\)
(a) Show that \(x^2-13x+42= 0\)
(b) Find the probability that Harper takes two right shoes.
30. | GCSE Higher |
There are only \(b\) blue counters and \(y\) yellow counters in a bag.
A counter is taken at random from the bag.
The probability that the counter is yellow is \( \frac{5}{8} \).
The counter is put back in the bag.
3 more blue counters and 6 more yellow counters are put in the bag.
A counter is taken at random from the bag.
The probability that the counter is blue is \( \frac{4}{11} \).
Find the number of blue counters and the number of yellow counters that were in the bag originally.
31. | IB Analysis and Approaches |
Let A and B be events such that \(P (A) = 0.45\) , \(P (B) = 0.35\) and \(P (A \cup B) = 0.5\).
Find \(P (A \mid B) \).
32. | IB Analysis and Approaches |
On a Tuesday at a theme park, a sample of 50 visitors was randomly selected as they were leaving the park. They were asked how many times that day they had been on a ride called The Serpent. This information is summarised in the following frequency table.
| Number of times on The Serpent | Frequency |
|---|---|
| 0 | 6 |
| 1 | 12 |
| 2 | 17 |
| 3 | 10 |
| 4 | 5 |
It can be assumed that this sample is representative of all visitors to the park for the following day.
(a) For the following day, Wednesday, estimate
(i) the probability that a randomly selected visitor will ride The Serpent;
(ii) the expected number of times a visitor will ride The Serpent.
It is known that 2000 visitors will attend the amusement park on Wednesday. The Serpent can carry a maximum of 18 people each time it runs.
(b) Estimate the minimum number of times The Serpent must run to satisfy demand.

33. | IB Analysis and Approaches |
Bag A contains 6 green tickets and 5 blue tickets.
Bag B contains 4 green tickets and 1 blue tickets.
(a) A bag is chosen at random and a ticket is drawn. Find the probability that the ticket is green.
Let J be the event that "bag A is chosen" and let K be the event that "a green ticket is drawn".
(b) Determine whether events J and K are independent.
34. | IB Standard |
Piers wins one of the many prizes on offer in the school raffle but he does not yet know exactly what the prize is.
Find the probability that the prize Piers wins is not both something to eat and worth more than $10 as Piers does not like expensive food.
35. | IB Standard |
The Venn diagram below shows the events \(A\) and \(B\), and the probabilities p, q and r.
It is known that \({\rm{P}}(A) = 0.43\) , \({\rm{P}}(B) = 0.62\) and \({\rm{P}}(A \cap B) = 0.27\) .
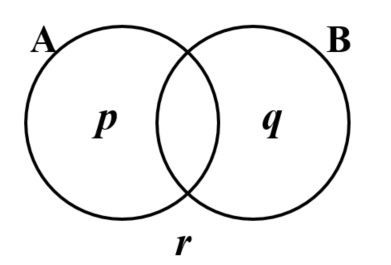
(a) Calculate the value of p.
(b) Calculate the value of q.
(c) Calculate the value of r.
(d) Find the value of \({\rm{P}}(A|B')\)
(e) Hence, or otherwise, show that the events \(A\) and \(B\) are not independent.
36. | IB Analysis and Approaches |
Events \(A\) and \(B\) are such that \(P(A) = 0.25\), \(P(A|B) = 0.15\) and \(P(A \cup B) = 0.65\).
Find \(P(B)\)
37. | IB Analysis and Approaches |
The heights, H metres, of flowers called Xylothorn Blooms growing in the dense forests of Verdantem on the luminous planet Aurorion can be modelled by a normal distribution with mean 14.3 metres and standard deviation 3.9 metres.

(a) One of the flowers is selected at random. Find the probability that its height more than 15.5 metres.
According to this model, 40% of the flowers have a height between \(x\) metres and 15.5 metres.
(b) Find the probability that a randomly selected flower has a height less than \(x\) metres.
(c) Find the value of \(x\).
(d) Ten flowers are selected at random.
Find the probability that no more than two of the flowers has a height less than \(x\) metres.
38. | IB Standard |
A game at a fayre consists of a players throwing one dart at the board pictured below.
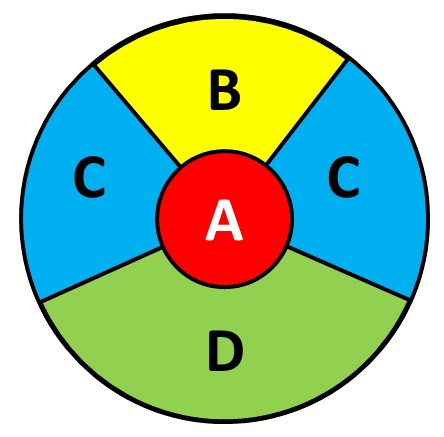
The probability of hitting each region and the points scored for hitting that region is given in this table.
| Region | Probability | Points |
|---|---|---|
| A | \(\frac{1}{25}\) | 50 |
| B | \(\frac{2}{25}\) | \(x\) |
| C | \(\frac{4}{25}\) | 20 |
| D | \(\frac{5}{25}\) | 10 |
(a) Find the probability that the dart does not hit the board.
The player scores points as shown in the table above but they lose 20 points if they miss the board completely.
(b) Given that the game is a fair game, find the value of \(x\), the number of points awarded for hitting the B region of the board.
39. | IB Studies |
Julie chooses a cake from a yellow box on a shelf. The box contains two chocolate cakes and three plain cakes. She eats the cake and chooses another one from the box. The tree diagram below represents the situation with the four possible outcomes where C stands for chocolate cake and P for plain cake.
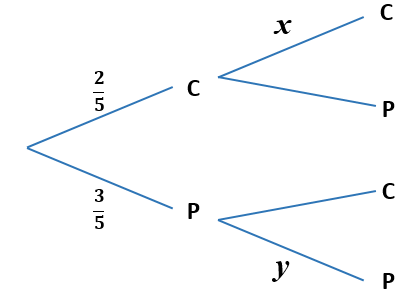
(a) Write down the value of \(x\).
(b) Write down the value of \(y\).
(c) Find the probability that both cakes are plain.
On another shelf there are two boxes, one red and one green. The red box contains four chocolate cakes and five plain cakes and the green box contains three chocolate cakes and four plain cakes. Ben randomly chooses either the red or the green box and randomly selects a cake.
(d) Copy and complete the tree diagram below.
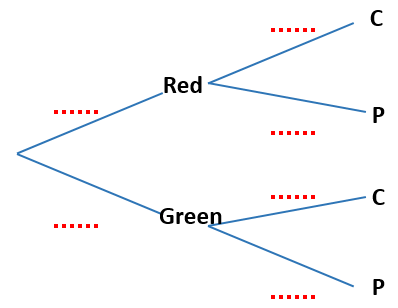
(e) Find the probability that he chooses a chocolate cake.
(f) Find the probability that he chooses a cake from the red box given that it is a chocolate cake.
40. | IB Standard |
Jane and David play two games of golf. The probability that Jane wins the first game is \(\frac56\). If Jane wins the first game, the probability that she wins the second game is \(\frac67\).
If Jane loses the first game, the probability that she wins the second game is \(\frac34\)
(a) Copy and complete the following tree diagram.

(b) Find the probability that Jane wins the first game and David wins the second game.
(c) Find the probability that David wins at least one game.
(d) Given that David wins at least one game, find the probability that he wins both games.
41. | IB Analysis and Approaches |
A continuous random variable \(X\) has probability density function \(f\) defined by
$$ f(x) = \begin{cases} \dfrac{1}{3q}, & 2q \le x \le 5q \\ 0, & \text{ otherwise } \end{cases}$$where \(q\) is a positive real number.
(a) State \(E(X)\) in terms of \(q\).
(b) Use integration to find \(Var(x)\) in terms of \(q\).
42. | IB Standard |
A random variable \(R\) has the probability distribution as shown in the following table:
| \(r\) | 1 | 2 | 3 | 4 | 5 |
| \(P(R=r)\) | 0.2 | a | b | 0.25 | 0.15 |
(a) Given that \(E(R) = 2.85\) find \(a\) and \(b\).
(b) Find \( P(R \gt 2 )\).
43. | IB Analysis and Approaches |
Amelia selects a disc from a bag containing 5 green discs, 4 blue discs and 3 red discs.
She wins £1 for a green disc, £3 for a blue disc, and £7 for a red disk. The game costs £4 to play.
(a) Calculate Amelia's expected gain for this game, and hence show that the game is not fair.
After a while, \(n\) red discs are added and Amelia wins £5 if she selects one. The game is now fair.
(b) Create an equation to represent this information.
(c) Hence, calculate the value of \(n\).
44. | IB Applications and Interpretation |
A game is played with a biased five-sided spinner. The possible scores, \(X\) and their probabilities are shown in the following table.
| Score \(x\) | -5 | -1 | 0 | 2 | 10 |
| \(P(X=x)\) | 0.2 | p | 0.3 | 0.3 | 0.1 |
(a) Find the exact value of p.
Jaedee plays the game once.
(b) Calculate the expected score.
Jaedee plays the game twice and adds the two scores together.
(c) Find the probability Jaedee has a total score of 10.
45. | IB Analysis and Approaches |
A factory manufactures switches. It is known that the probability that a switch is found to be defective is 0.04. A random sample of 50 switches is tested.
(a) Find the probability that there is at least one defective switch in the sample.
(b) Given that there is at least one defective switch in the sample, find the probability that there are at least three defective switches.
46. | IB Standard |
A famous pole vaulter finds that she is successful on 85% of her attempts at clearing five metres. Her Wikipedia entry confirms that her success rate is 85%.

A field sports day event consists of 12 five-metre vaults.
a) Find the probability that she is successful on all 12 attempts.
b) Find the probability that she is successful on at least 8 attempts.
She can earn £50 in prize money for every successful vault
c) What can she expect her winnings to be in a one day event?
The probability that another vaulter is successful at clearing five metres 3 times out of 12 is 0.166.
d) What are the possible value(s) of his success rate?
47. | IB Analysis and Approaches |
At a fitness club, \( 60\% \) of the members are full-time members, and \( 30\% \) of the members participate in group fitness classes. \( 25\% \) of the members are neither full-time members nor participate in group fitness classes.
A member is selected at random.
(a) Find the probability that the member is a full-time member and participates in group fitness classes.
(b) Find the probability that the member participates in group fitness classes, but is not a full-time member.
In the club, \( 50\% \) of the members are male, and \( 40\% \) of the male members participate in group fitness classes.
A member is selected at random. Let \( M \) be the event "the member is male" and let \( F \) be the event "the member participates in group fitness classes".
(c) Find \( P(M \cap F) \).
(d) Determine if the events \( M \) and \( F \) are independent. Justify your answer.

48. | IB Analysis and Approaches |
A continuous random variable \( X \) has the probability density function \( f_n \), given by
$$ f_n(x) = \begin{cases} (n+3)x^2 - \dfrac{2nx}{3}, & 0 \leq x \leq 1 \\ 0, & \text{otherwise} \end{cases} $$where \( n \in \mathbb{R}, n \geq 0 \).
(a) Show that \( E(X) = \dfrac{n + 27}{36} \).
(b) Show that \( \text{Var}(X) = \dfrac{n + 18}{30} - \left(\dfrac{n + 27}{36}\right)^2 \).
49. | A-Level |
Mathsland's national currency comes in denominations of 1 unit, 5 units, 10 units and 50 units. Sofya places this collection of these coins in her purse then, without looking, takes out two coins at random, one after the other.
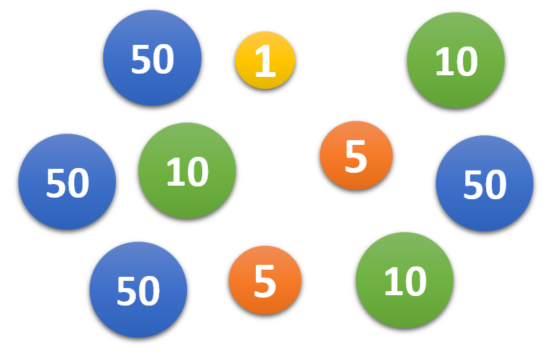
Draw a tree diagram to represent the situation and then use it to calculate the probability that the second coin that Sofya takes out of her purse has a greater value than the first.
50. | IB Standard |
Two events A and B are such that \(P(A) = 0.57\) and \(P (A \cap B) = 0.21\).
(a) Find \(P (A \cap B' ) \).
(b) Given that \(P((A \cup B)') = 0.17 \), find \(P(A|B')\).
51. | IB Analysis and Approaches |
Some orange fish and green fish are swimming in a large tank in the enterance to a restaurant. The number of orange fish is a single digit number as is the number of green fish.

The chef occasionally takes a fish from the tank at random. So far today he has taken out two fish.
The tank initially contains r orange fish and g green fish.
Let \( P(GG) \) represent the probability of drawing two green fish from the tank without replacement.
It is known that \( P(GG) = \frac{1}{5} \).
(a) Show that \( 4g^2 - (4 + 2r)g + r - r^2 = 0 \).
(b) By solving the equation in part (a), show that \( g = \dfrac{(2+r) \pm \sqrt{5r^2 + 4}}{4} \).
(c) Find two pairs of values for r and g that satisfy the condition \( P(GG) = \frac{1}{5} \).
On a different day the chef randomly takes three fish out of the tank. The tank initially contained 10 orange fish and g green fish.
Let \( P(GGG) \) represent the probability of taking three green fish from the tank without replacement.
(d) Find an expression for \( P(GGG) \) in terms of g.
A green fish is added so that the tank now contains 10 orange fish and \( g + 1 \) green fish. The probability of taking three green fish from the tank without replacement is now twice the probability expressed in part (d).
(e) Find the initial number of green fish in the tank on this particular day.
52. | IB Analysis and Approaches |
A red spinner is designed with five possible outcomes. Let \(X\) be the score obtained when the spinner is spun. The probability distribution for \(X\) is given in the following table.
| \(x\) | 3 | 4 | 5 | 8 | 10 |
| \(P(X=x)\) | \(p\) | \(2p\) | \(p\) | \(2p\) | \(p\) |
(a) Find the value of p.
(b) Find the value of \(E(x)\).
A blue spinner is also designed with five possible outcomes. Let \(Y\) be the score obtained when the spinner is spun. The probability distribution for \(Y\) is given in the following table.
| \(y\) | 1 | 2 | 3 | 4 | 5 |
| \(P(Y=y)\) | \(r\) | \(r\) | \(q\) | \(q\) | \(q\) |
(c) State the range of possible values of \(q\).
(d) State the range of possible values of \(r\).
(e) Hence find the range of possible values of \(E(Y)\).
Arnold and Bernie play a game using these spinners. Arnold spins the red spinner once and Bernie spins the blue spinner once. The probability that Arnold's score is less than Bernie's score is \(\frac{1}{7}\).
(f) Find the value of \(E(Y)\).
53. | IB Standard |
The length of Costlow's bâtard bread loaves in centimetres is normally distributed with mean \( \mu \). The following table shows probabilities for values of \(L\).
| Length (\(L\)) | \(L \lt 30\) | \(30 \le L \le 42\) | \(L \gt 42\) |
|---|---|---|---|
| P(X) | 0.07 | 0.86 | \(k\) |
(a) Calculate the value of \(k\).
(b) Show that \( \mu \) = 36.
(c) Find P(\(L \gt 39\)).
The loaves are displayed in baskets of twelve. Any loaves with a length less than 31cm are classified as short.
(d) Find the probability that a basket of loaves selected at random contains at most one loaf that is short.
(e) Each Costlow supermarket has 40 baskets of loaves. One of the Costlow supermarkets is selected at random. Find the expected number of baskets in this supermarket that contain at most one loaf that is too short.
(f) Find the probability that at least 28 baskets in this supermarket contain at most one loaf that is too short.

54. | IB Analysis and Approaches |
The continuous random vanable \(X\) has probability density function:
$$ f(x) = \begin{cases} \dfrac{k}{\sqrt{16-x^2}}, & 0 \le x \le 2 \\ 0, & \text{ otherwise } \end{cases}$$(a) Find the value of \(k\)
(b) Show that \(E(X) = \dfrac{12(2-\sqrt{3})}{\pi}\)
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.