Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Steps Investigate the numbers associated with this growing sequence of steps made from Multilink cubes.
Steps Investigate the numbers associated with this growing sequence of steps made from Multilink cubes. Missing Terms Can you work out which numbers are missing from these number sequences?
Missing Terms Can you work out which numbers are missing from these number sequences? Leapfrog An investigation of the minimum number of moves required to make the blue and green frogs swap places.
Leapfrog An investigation of the minimum number of moves required to make the blue and green frogs swap places.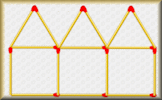 Matchstick Patterns Create a formula to describe the nth term of a sequence by examining the structure of the diagrams.
Matchstick Patterns Create a formula to describe the nth term of a sequence by examining the structure of the diagrams. Sequence Generator An online app which produces number sequences as words.
Sequence Generator An online app which produces number sequences as words.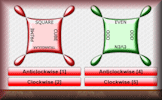 Watsadoo Rotate the cogs to catch the flying numbers in the correct sections.
Watsadoo Rotate the cogs to catch the flying numbers in the correct sections. Arithmetic Sequences An exercise on linear sequences including finding an expression for the nth term and the sum of n terms.
Arithmetic Sequences An exercise on linear sequences including finding an expression for the nth term and the sum of n terms.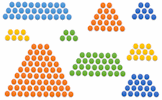 Trapezia Which numbers can be represented by groups of circles arranged in the shape of a trapezium?
Trapezia Which numbers can be represented by groups of circles arranged in the shape of a trapezium?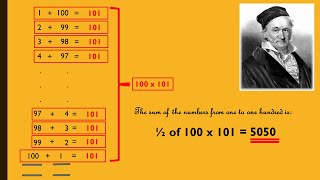 Arithmetic Sequences Video A reminder of how to find the next term, the nth term and the sum of terms of an arithmetic or linear sequence.
Arithmetic Sequences Video A reminder of how to find the next term, the nth term and the sum of terms of an arithmetic or linear sequence. Prison Cell Problem A number patterns investigation involving prisoners and prison guards.
Prison Cell Problem A number patterns investigation involving prisoners and prison guards. Geometric Sequences An exercise on geometric sequences including finding the nth term and the sum of any number of terms.
Geometric Sequences An exercise on geometric sequences including finding the nth term and the sum of any number of terms. Geometric Sequences Video Revise all you need to know about geometric sequences and series.
Geometric Sequences Video Revise all you need to know about geometric sequences and series. Aunt Lucy's Legacy Decide which of the four schemes Aunt Lucy proposes will provide the most money. This investigation involves the sum of sequences as well as considering life expectancy.
Aunt Lucy's Legacy Decide which of the four schemes Aunt Lucy proposes will provide the most money. This investigation involves the sum of sequences as well as considering life expectancy. Fibonacci Quest A number of self marking quizzes based on the fascinating Fibonacci Sequence.
Fibonacci Quest A number of self marking quizzes based on the fascinating Fibonacci Sequence. Handshakes If everyone in this room shook hands with each other, how many handshakes would there be?
Handshakes If everyone in this room shook hands with each other, how many handshakes would there be?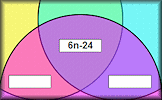 Venn Diagram of Sequences Find the formula for the nth term of sequences that belong in the given sets.
Venn Diagram of Sequences Find the formula for the nth term of sequences that belong in the given sets.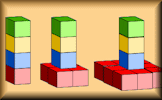 Quadratic and Cubic Sequences Deduce expressions to calculate the nth term of quadratic and cubic sequences.
Quadratic and Cubic Sequences Deduce expressions to calculate the nth term of quadratic and cubic sequences. Sequences Table Challenge Complete the table showing the terms of the sequences and the formulas for the nth terms.
Sequences Table Challenge Complete the table showing the terms of the sequences and the formulas for the nth terms.
Here are some exam-style questions on this statement:
- "The first five terms of an arithmetic sequence are:" ... more
- "Here is a picture of four models. Some of the cubes are hidden behind other cubes." ... more
- "In a sequence" ... more
- "(a) Find the \(n\)th term of the sequence 7, 13, 19, 25,..." ... more
- "A large mug of hot tea is cooling on a small lounge table." ... more
- "Work out an expression for the nth term of the quadratic sequence" ... more
- "Here are the first six terms of a quadratic sequence." ... more
- "Find an expression, in terms of \(n\), for the \(n\)th term of the sequence that has the following first five terms:" ... more
- "Here are the first six terms of a quadratic sequence." ... more
- "The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre." ... more
- "The diagrams below show a sequence of patterns made from red and yellow tiles." ... more
- "(a) A sequence is defined by the following rule where \(u_n\) is the \(n^{th}\) term of the sequence:" ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Number Spotting patterns is an important skill in many areas of life. The world of numbers contains many fascinating patterns and understanding them enables better problem solving strategies. From seeing patterns in the multiples of numbers shaded in a hundred square to spotting the recurring sequences of digits in decimal numbers there is a great deal for pupils to be introduced to. This topic includes even, odd, prime, triangular, perfect, abundant, square and cube numbers. It uses factors and multiples to find solutions to real life problems and encourages number connections to be investigated for pleasure. There are a lot of puzzles, challenges and games too. See also the Mental Methods topic and our Number Skills Inventory.
- Sequences A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them. The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms. Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom. Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

