

What is the 10th:
a) Odd number; 19
b) Square number; 100
c) Prime number. 29
Find all the factors of:
23
1, 23.
Subtract the 4th from the 8th multiples of:
5
20
What are the names of regular polygons with:
a) five sides;
b) six sides;
c) seven sides.
Pentagon, Hexagon and Heptagon (all regular)
Round to three significant figures:
a) 50.35; 50.3
b) 368576; 369000
c) 85; 85.0
d) 0.008595; 0.00860
Find the area of a triangle that has a base of 7cm and a height of 12cm.
42cm2
Find the area of a trapezium that has a base of 11cm, a height of 10cm and a top (parallel to base) of 5cm. 80cm2
Evaluate:
\( \frac{1}{4} + \frac{6}{9}\) \(= \frac{11}{12}\)
Evaluate:
\( \frac{1}{2} × \frac{4}{6}\) \(= \frac{1}{3}\)
Evaluate:
\( \frac{2}{3} ÷ \frac{6}{4}\) \(= \frac{4}{9}\)
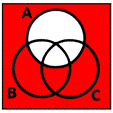
Name the red part.


Describe the red region.

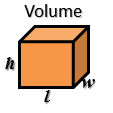
What is the formula?
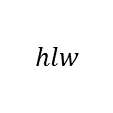
What is it?

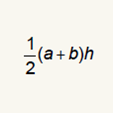
Convert this fraction to a percentage to 3 significant figures.
\( \frac{1}{6}\) \(= 16.7\)%
Find the area of a circle that has a radius of 9cm. Give your answer to three significant figures.
254cm2
Find the circumference of a circle that has a radius of 2cm. Give your answer to three significant figures.
12.6cm
Calculate the value of:
7.5 + 4.6
= 12.1
Calculate the value of:
5.1 − 3.7
= 1.4
Calculate the value of:
8.9 × 5.4
= 48.06
Calculate the value of:
41.6 ÷ 13
= 3.2
What is the value of:
13
= 1
What is the value of:
\(4^{-3}\)
\(= \frac{1}{64}\)
Calculate the value of:
88 + 98
= 186
Calculate the value of:
81 − 25
= 56
Calculate the value of:
82 × 32
= 2624
Calculate the value of:
2304 ÷ 24
= 96
Find the value of:
75% of 280
= 210
Find the value of:
4.11 × 103
= 4110
Find the highest common factor of forty and ten.
= 10
9 × 5 = 45 | 6 × 2 = 12 |
5 × 2 = 10 | 3 × 3 = 9 |
4 × 5 = 20 | 7 × 3 = 21 |
8 × 5 = 40 | 2 × 2 = 4 |
7 × 6 = 42 | 8 × 10 = 80 |
4 × 9 = 36 | 3 × 5 = 15 |
5 × 12 = 60 | 6 × 12 = 72 |
9 × 11 = 99 | 2 × 9 = 18 |
3 × 2 = 6 | 7 × 2 = 14 |
8 × 2 = 16 | 4 × 2 = 8 |
9 × 2 = 18 | 6 × 2 = 12 |
5 × 2 = 10 | 2 × 2 = 4 |
6 × 3 = 18 | 5 × 3 = 15 |
4 × 3 = 12 | 9 × 3 = 27 |
7 × 3 = 21 | 8 × 3 = 24 |
3 × 3 = 9 | 2 × 3 = 6 |
5 × 4 = 20 | 7 × 4 = 28 |
9 × 4 = 36 | 6 × 4 = 24 |
3 × 4 = 12 | 8 × 4 = 32 |
4 × 4 = 16 | 2 × 4 = 8 |
3 × 5 = 15 | 5 × 5 = 25 |
6 × 5 = 30 | 8 × 5 = 40 |
9 × 5 = 45 | 7 × 5 = 35 |
4 × 5 = 20 | 2 × 5 = 10 |
8 × 6 = 48 | 6 × 6 = 36 |
9 × 6 = 54 | 5 × 6 = 30 |
3 × 6 = 18 | 4 × 6 = 24 |
7 × 6 = 42 | 2 × 6 = 12 |
3 × 7 = 21 | 9 × 7 = 63 |
6 × 7 = 42 | 5 × 7 = 35 |
7 × 7 = 49 | 4 × 7 = 28 |
8 × 7 = 56 | 2 × 7 = 14 |
5 × 8 = 40 | 6 × 8 = 48 |
8 × 8 = 64 | 3 × 8 = 24 |
4 × 8 = 32 | 9 × 8 = 72 |
7 × 8 = 56 | 2 × 8 = 16 |
8 × 9 = 72 | 3 × 9 = 27 |
4 × 9 = 36 | 7 × 9 = 63 |
5 × 9 = 45 | 6 × 9 = 54 |
9 × 9 = 81 | 2 × 9 = 18 |
8 × 12 = 96 | 7 × 12 = 84 |
6 × 12 = 72 | 5 × 12 = 60 |
3 × 12 = 36 | 9 × 12 = 108 |
4 × 12 = 48 | 2 × 12 = 24 |
Write this fraction in its simplest form:
\( \frac{32}{40}\) \(= \frac{4}{5}\)
Evaluate:
\( 1\frac{2}{3} − \frac{6}{7}\) \(= \frac{17}{21}\)
Find BC if AB = 3.3m and AC = 4.9m. 5.91m
Find angle ABC if AC = 5.4m and AB = 6.4m. 40.2o
Find AC if angle ABC = 59o and BC = 5.7m. 4.89m
Give your answer in Roman numerals.
2
Give your answer in Roman numerals.
2
Give your answer in Roman numerals.
2
Convert this fraction to a decimal.
\( \frac{5}{10}\) \(= 0.5\)
Convert this decimal to a fraction.
\(0.23\) = \( \frac{23}{100}\)
Increase £160 by 10%
£176
What is the lowest common multiple of twelve and twenty eight.
= 84
2,11,20,29,38...
Find the:
a) next term; 47
b) nth term; 9n - 7
c) term number 38; 335
3,6,12,24,48...
Find the:
a) next term; 96
b) nth term; 3 × 2n-1
c) term number 10; 1536
If £200 is invested for 9 years with a simple interest rate of 4%, find the amount of interest earned. £72.00
If £220 is invested with an interest rate of 3% compounded annually, find the value of the investment after 6 years. £262.69
If £1 is worth $1.25, convert:
a) £200 to dollars; $250.00
b) $160 to pounds; £128.00
What are the coordinates of the midpoint of the line joining:
\((4,3) \text{ and } (12,11)\)
(8,7)
What is the gradient of the line joining:
\((5,8) \text{ and } (10,11)\)
\(\frac{3}{5}\)
Here are the coordinates of 3 vertices of a square, what are the coordinates of the 4th?
\((4,3),(10,8),(-1,9)\)
(5,14)
a) 5 − 14 = -9
b) 5 × (-7) = -35
c) (8−14)(8−19) = 66
d) 35 ÷ (-7) = -5
e) (-10)2 = 100
If p = 6, q = 19 and
r = -12 evaluate:
a) 2q − p = 32
b) pq + r = 102
c) p2 − 5q - r = -47
Solve:
\(5x = 20\)
\(x = 4\)
Solve:
\(5x +3= 33\)
\(x = 6\)
Solve:
\(4x -4= 2x + 12\)
\(x = 8\)
Solve:
\(4(3x +2)-8= 96\)
\(x = 8\)
Solve:
\(4(4x + 2)= 3(5x + 4)\)
\(x = 4\)
Solve:
\(3x+5y = 48\)
\(4x+5y = 54\)
\(x = 6, y = 6\)
Solve:
\(2x+3y = 17\)
\(7x-12y = -8\)
\(x = 4, y = 3\)
Solve:
\(5x-5y = -57.5\)
\(3x-2y = -30\)
\(x = -7, y = 4.5\)
Find the union of:
{6,7,8,9,10} and
{2,6,12}
{2,6,7,8,9,10,12}
Find the intersection of:
{6,7,8,9,10} and
{3,4,5,6,7,8}
{6,7,8}
A plane flies from point A to point B on a bearing of 174o. What bearing would it return on from B to A? 354o
A number is picked at random from the set
{1,3,6,10,15}
what is the probability it is even? \(\frac25\)
Evaluate:
63 ÷ 9 × 42 ÷ 7
42
Simplify the following by collecting like terms:
\(6m+7+5m+8\)
\(11m+15\)
Divide 56 in the ratio
1:6
8 and 48
Draw a rough sketch of the graph of:
\(y=-2x+1\)
Gradient -2
y intercept 1
Express the following number as the product of prime numbers:
18
2 x 3 x 3
In a sale an item costs £12 after a 40% reduction. What was the original price?
£20
Find the mean, mode, median and range of the following:
5,6,7,8,9,10
Mean = 7.5, no mode,
median = 7.5 and range = 5
What time is this?
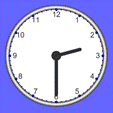

Sketch a clock face:


Write the following recurring decimal as a fraction in its lowest terms.
0.373737... \(\frac{37}{99}\)
Decrease £140 by 25%
£105
Expand:
\(2(3x-3)\)
\(6x-6\)
Expand:
\((4x+2)(3x-3)\)
\(12x^2-6x-6\)
Factorise:
\(12x-6\)
\(6(2x-1)\)
Factorise:
\(x^2+x-12\)
\((x+4)(x-3)\)
Factorise:
\(2x^2+x-1\)
\((x+1)(2x-1)\)
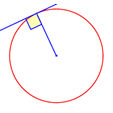
Which theorem?

Find the value of:
5.1 × 10-4
= 0.00051
Write in standard form:
892000
= 8.92 × 105
Write in standard form:
0.0979
= 9.79 × 10-2
Find the nth term:
\(-3, 5, 17, 33, 53, \)
\(2n^2+2n-7\)
Multiply 8 × 104
by 8 × 105 and give the answer in standard form.
= 6.4 × 1010
Solve:
\(x^2+2x-15= 0\)
\(x = 3\) and \(-5\)
Solve this equation giving the solutions to 3 significant figures:
\(2x^2+x-5 = 0\)
\(x = 1.35\) and \(-1.85\)
What is the size of each interior angle of a regular hexagon?
120°
Make \(k\) the subject of the formula
$$c=\frac{a(2+k)}{b}$$
$$k=\frac{bc}{a}-2$$
Calculate the value of:
2824 ÷ 4
= 706
What is the 11th:
a) Cube number; 1331
b) Triangular number; 66
c) Fibonacci number. 89
What is the square of
3
9
What are the three largest prime numbers less than
41
37, 31, 29
Write down something you learnt in the previous mathematics lesson.
Write down something you learnt in one of the mathematics lessons last week.
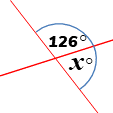
Calculate \(x\).
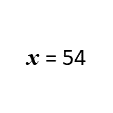
Write down these numbers: 9, 9.99, 9.9, 0.99, 0.9, 9.09, 0.09, in ascending order.
0.09, 0.9, 0.99, 9, 9.09, 9.9, 9.99,
Write down these lengths: 1.08m, 18mm, 107cm, 17cm, 1.8m, 1.7cm, in order.
1.7cm, 18mm, 17cm, 107cm, 1.08m, 1.8m,
Write down these capacities: 17cl, 18cl, 200ml, 21cl, 173ml, 18ml, in order.
18ml, 17cl, 173ml, 18cl, 200ml, 21cl,


Round to one significant figure:
a) 71.54; 70
b) 468934; 500000
c) 32; 30
d) 0.00243; 0.002
Round each value to one significant figure to make an estimate:$$(173 + 5.7) \div 17$$\((200 + 6) \div 20 = 10.3\)
A pie chart shows the colours of 12 books. What sector angle represents the
5 red books?
150°
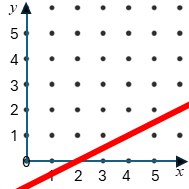
What is the equation?
\(y=0.5x-1\)A pie chart shows the colours of 40 hats. How many green hats are represented
by a sector
angle of 270°?
30
Simplify:
$$\sqrt{32}$$
\(4\sqrt{2}\)
Simplify:
$$\dfrac{7}{\sqrt{5}}$$\(\frac{7\sqrt{5}}{5}\)
Simplify:
$$\dfrac{8}{3 + \sqrt{6}}$$\(\frac{24 - 8\sqrt{6}}{3}\)
Topics: Starter | Algebra | Arithmetic | Circles | Coordinates | Fractions | Mental Methods | Mixed | Money | Sets | Simultaneous Equations | Tables | Trigonometry
How did you use this starter? Can you suggest
how teachers could present or develop this resource? Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for Maths teachers anywhere in the world.
Click here to enter your comments.
Previous Day | This starter is for 9 April | Next Day
Tick (or untick) the boxes above to select the concepts you want to be included in this Starter [untick all]. The display at the top of this page will change instantly to show your choices. You can also drag the panels above so that the questions are ordered to meet your needs.
This Starter is called Refreshing Revision because every time you refresh the page you get different revision questions.
Regularly use this Starter to keep that important learning from being forgotten. Here is the web address (URL) for the version of this page with your currently selected concepts:
Copy and paste the URL above into your lesson plan or scheme of work.
For more ideas on revision there are plenty of tips, suggestions and links on the Mathematics Revision page.

|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=April9 However it would be better to assign one of the student interactive activities below. |
|
Here is the URL which will take them to a related student activity.
Try this Uniqueness Game with your class.
Here's a projectable set of randomly-selected revision questions for the end of the lesson.