Cookies are used on this website.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

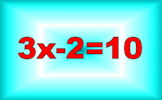• Equations A series of exercises, in increasing order of difficulty, requiring you to solve linear equations. The exercises are self marking.
• eQuation Generator An unlimited supply of linear equations just waiting to be solved. Project for the whole class to see then insert the working in your own style.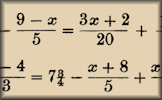
• Old Equations Solve these linear equations that appeared in a book called A Graduated Series of Exercises in Elementary Algebra by Rev George Farncomb Wright published in 1857.
• Simultaneous Shopping Find the cost of the individual items in shopping baskets (introduction to simultaneous equations).
• Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.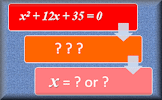
• Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.
• Simultaneous Equations Video Learn to solve simultaneous equations from the very basic to those containing quadratics. This video is to help you do the online, self-marking exercise.
• Simultaneous Equations A self-marking, multi-level set of exercises on solving pairs of simultaneous equations.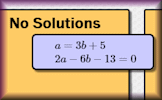
• Simultaneous Solutions Arrange the given pairs of simultaneous equations in groups to show whether they have no solution, one solution or infinite solutions.
• Unbeknownst Some picture grid puzzles which can be solved by using simultaneous equations.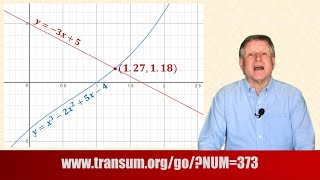
• Simultaneous Graphs Video A short video which explains how to use graphs to solve simultaneous equations.

Here are some exam-style questions on this statement:

• "The diagram shows an isosceles triangle (not drawn to scale)." ... more
• "Solve the following linear equation to find the value of \(x\)." ... more
• "The trapezium and rectangle shown here have the same perimeters. The diagrams are not drawn to scale and the measurements are in centimetres. Calculate the area of the trapezium." ... more
• "Solve the simultaneous equations" ... more
• "Solve the simultaneous equations:" ... more
• "The area of rectangle PQRS (not to scale) is 80cm². " ... more
• "(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\)." ... more
• "A rectangular sheet of paper can be cut into two identical rectangular pieces in two different ways, either by cutting along line A or by cutting along line B." ... more
• "Show that you understand equations and inequalities by answering the following:" ... more
• "A red rug has a width of \(x-3\) cm and a length of \(4x\) cm." ... more
• "Two numbers are chosen so that the sum of their squares is 25." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
• Simultaneous Equations This topic covers simultaneous equations with two different variables. The starters pose real world problems which can be solved using the techniques taught at school or by other intuitive methods. Though there are many formal strategies for solving simultaneous equations the skill of forming the equations from real life situations is a very important stage in working towards a solution. Algebraic methods are the most efficient for solving basic simultaneous equations but graphical methods, probably using a graphic display calculator or computer software package, may be more suitable for less standard sets of simultaneous equations.