Cookies are used on this website.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

• Mix and Math Determine the nature of adding, subtracting and multiplying numbers with specific properties.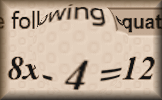
• Words and Concepts Fill in the missing words to show an understanding of the vocabulary of equations, inequalities, terms and factors.
• Identity, Equation or Formula? Arrange the given statements in groups to show whether they are identities, equations or formulae.
• True or False? Arrange the given statements in groups to show whether they are always true, sometimes true or false.

Here are some exam-style questions on this statement:

• "State whether each of the following statements is true or false. Give reasons for your answers." ... more
• "One is added to the product of two consecutive positive even numbers. Show that the result is a square number." ... more
• "(a) Give a reason why 0 is an even number." ... more
• "Betsy thinks that \((3x)^2\) is always greater than or equal to \(3x\)." ... more
• "This expression can be used to generate a sequence of numbers." ... more
• "Given that \(n\) can be any integer such that \(n \gt 1\), prove that \(n^2 + 3n\) is even." ... more
• "m and n are positive whole numbers with m > n" ... more
• "Express as a single fraction and simplify your answer." ... more
• "(a) Prove that the product of two consecutive whole numbers is always even." ... more
• "The number \(T\) can be expressed as \(T = 4k + 3\) where \(k\) is a positive integer." ... more
• "Prove that the expression below is always positive." ... more
• "Consider the sum of the squares of any two consecutive odd integers." ... more

See all these questions

Here is an Advanced Starter on this statement:

• Two Equals One
  What is wrong with the algebraic reasoning that shows that 2 = 1 ? more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".