Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Cartoon Scatter Graph Place the cartoon characters on the scatter graph according to their height and age.
Cartoon Scatter Graph Place the cartoon characters on the scatter graph according to their height and age. Estimating Correlation Practise the skill of estimating the correlation of data on a scatter graph in this self marking exercise.
Estimating Correlation Practise the skill of estimating the correlation of data on a scatter graph in this self marking exercise. Correlation Arrange the given statements in groups to show the type of correlation they have.
Correlation Arrange the given statements in groups to show the type of correlation they have. Human Scatter Graphs Pupils move to positions in the room according to their data relative to the walls as axes.
Human Scatter Graphs Pupils move to positions in the room according to their data relative to the walls as axes. Plotting Scatter Graphs Plot scatter graphs from data representing a number of different everyday situations.
Plotting Scatter Graphs Plot scatter graphs from data representing a number of different everyday situations.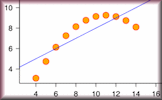 Odd Scatter Out Just by looking at the scatter graphs can you decide which is the odd one out according to their summary statistics?
Odd Scatter Out Just by looking at the scatter graphs can you decide which is the odd one out according to their summary statistics?
Here are some exam-style questions on this statement:
- "The number of visitors to a cycle track and the number of drinks sold by a café at the location are recorded in the table below." ... more
- "The scatter graph shows the maximum temperature (oC) and the number of bowls of soup sold at a sandwich shop on twelve randomly selected days last year." ... more
- "The following table shows the relationship between the number of workers and the amount of time in minutes it takes them to harvest the sugar cane in a particular field." ... more
- "The following table shows the amount of diesel required by a train to travel certain distances." ... more
- "The following table shows the weight in kilograms of members of a group of young children of various ages." ... more
- "The following table shows the average number of hours per night sleeping by seven men and their youngest child." ... more
- "Miss Chloe Sharpe (singing teacher) was teaching nine students last year. At the end of the year the students took a singing exam and their results were reported as percentages. Chloe decided to record the average number of hours per week each student reported practising in the weeks before the examination." ... more
- "A programmer recorded the number of web pages she had created since she had begun working for the Corney Content Creation Company. The following table shows the number of days, \(d\), and the cumulative total number of web pages, \(p\)." ... more
- "The following table shows the average weights for given heights in a population of men." ... more
- "Data is collected about size in square metres of apartments in a city and the monthly cost of renting them. The size of the apartments is shown in this box and whisker diagram." ... more
- "Ten students are given a test on calculus and a test on probability. Each test is scored out of a total of 100 marks. The scores of the students are shown in the following table:" ... more
- "As part of a conservation project, Darren was asked to measure the circumference of trees that were growing at different distances from a beach.
His results are shown in the following table.
" ... more - "At a large airport, the waiting time between a plane landing and a passenger being able to get off the aircraft is dependent upon the row number of the seat that the passenger has been assigned to." ... more
- "The Farang Parkour Team hosted a Free Running event. The judges, Anan and Jason awarded 7 competitors a score out of 10. The scores are shown in the following table." ... more
- "In a survey of insect life near a stream, a student collected data about the number of different insect species \((y)\) that were found at different distances \((x)\) in metres from the stream." ... more
- "A pair of twins, Percy and Patsy, take Maths assessment tests each week. Their teacher records their scores in this table:" ... more
- "The table below shows the scores for 12 students on two Mathematic exam papers. For the first paper calculators were allowed and for the second paper they were not." ... more
- "A community leader is monitoring the state of flood water levels in a local area." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Linear correlation of bivariate data refers to the strength and direction of a linear relationship between two variables. When two variables tend to increase or decrease together in a consistent manner, they are said to have a linear correlation. Pearson’s product-moment correlation coefficient, denoted as \( r \), quantifies the strength and direction of this linear relationship. The value of \( r \) lies between -1 and 1, with -1 indicating a perfect negative linear relationship, 1 indicating a perfect positive linear relationship, and 0 indicating no linear relationship.
Scatter diagrams, also known as scatter plots, are graphical representations of bivariate data. Each point on the scatter diagram represents a pair of values for the two variables. The pattern of points can give an indication of the type and strength of the relationship between the variables.
The equation of the regression line of \( y \) on \( x \), also known as the least squares regression line, provides a linear model that best fits the data points in a scatter diagram. This line can be used to make predictions about \( y \) based on values of \( x \).
Key formulae [In the exam a GDC would be used to calculate r and to find the equation of the regression line].
$$ r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} $$
Where:
\( r \) = Pearson’s product-moment correlation coefficient
\( x_i \) and \( y_i \) = Individual data points
\( \bar{x} \) and \( \bar{y} \) = Means of \( x \) and \( y \) respectively
Equation of the regression line of \( y \) on \( x \):
$$ y = a + bx $$
Where:
\( b = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} \)
and
\( a = \bar{y} - b\bar{x} \)
If you use the TI-Nspire calculator you can find instructions for finding the regression line on the GDC Essentials page. The equation of that line can then be used for prediction purposes.
THE CORRELATION COEFFICIENT (r)
| Value | Strength of Association |
|---|---|
| \( r = -1 \) | perfect negative correlation |
| \( -1 \lt r \le -0.90 \) | very strong negative correlation |
| \( -0.90 \lt r \le -0.75 \) | strong negative correlation |
| \( -0.75 \lt r \le -0.50 \) | moderate negative correlation |
| \( -0.50 \lt r \le -0.25 \) | weak negative correlation |
| \( -0.25 \lt r \lt 0 \) | very weak negative correlation |
| \( r = 0 \) | no correlation |
| \( 0 \lt r \lt 0.25 \) | very weak positive correlation |
| \( 0.25 \le r \lt 0.50 \) | weak positive correlation |
| \( 0.50 \le r \lt 0.75 \) | moderate positive correlation |
| \( 0.75 \le r \lt 0.90 \) | strong positive correlation |
| \( 0.90 \le r \lt 1 \) | very strong positive correlation |
| \( r = 1 \) | perfect positive correlation |
This Bicen Maths video clip shows everything you need to memorise on Regression and Correlation for A Level Statistics.
This video on Bivariate Statistics is from Revision Village and is aimed at students taking the IB Maths AA SL/HL level course.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

