GCSE Mathematics Syllabus Statement

Subject Content:

Pupils should be taught to simplify and manipulate algebraic expressions (including those involving surds {and algebraic fractions}) by: factorising quadratic expressions of the form x² + bx + c, including the difference of 2 squares; {factorising quadratic expressions of the form ax² + bx + c} and by simplifying expressions involving sums, products and powers, including the laws of indices

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

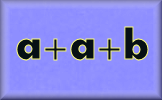Algebraic Notation Simplification using the normal conventions of algebra.

Collecting Like Terms Video If you have forgotten what collecting like terms means watch this video for a quick refresher.

Collecting Like Terms Practise your algebraic simplification skills with this self marking exercise.

Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations.

Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication.

How old was Diophantus? An ancient riddle which can be answered by solving an equation containing fractions.

Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level.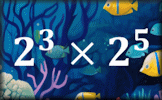

Power Play Exercises on powers and roots and simplifying index expressions involving numbers of the same base.

Algebraic Fractions A mixture of algebraic fraction calculations and simplifications.

Here are some exam-style questions on this statement:

"Multiply out and simplify:" ... more

"Simplify the following algebraic fraction:" ... more

"Simplify the following expressions:" ... more

"Factorise the following expression:" ... more

"(a) Simplify:" ... more

"Find the highest common factor of the following two expressions:" ... more

"Simplify then find the square root of this expression:" ... more

"(a) The expression \( (x+1)(2x-3)(3x+4) \) can be written in the form \(ax^3 + bx^2 + cx + d \) where \(a, b, c\) and \(d\) are integers. Find the values of \(a, b, c\) and \(d\)." ... more

"(a) Simplify \( \left(\dfrac{3a}{a^3 - 3}\right)^0 \)" ... more

"Work out the exact value of \(n\)." ... more

"(a) Express the following as a single fraction in its simplest form." ... more

"(a) Simplify \( 6(3a-2)-2(a-3) \)" ... more

"(a) The \(n\)th term of a sequence is \(2^n+2^{n+1}\)" ... more

"(a) Simplify the following expression." ... more

"(a) Without using a calculator, show that \(\sqrt{28}=2\sqrt7\)

(b) The point \(X\) is shown on the unit grid below. The point \(Y\) is \(\sqrt17\) units from \(X\) and lies on the intersection of two grid lines. Mark one possible position for \(Y\)." ... more

"If a, b and c are positive integers use the following statements to find the values of a, b and c." ... more

"Factorise the following expression" ... more

"Show that:" ... more

"The expression below can be written as a single fraction in the form \( \dfrac{a-bx}{x^2-25} \) where \(a\) and \(b\) are integers." ... more

"\(y = a \times b^{x – 2}\) where \(a\) and \(b\) are numbers." ... more

See all these questions

Here are some Advanced Starters on this statement:

Algebraic Product
Finding the value of the expression is easier than you think! more

Paper Ratio
Calculate the ratio of the sides of an A4 sheet of paper without any measuring. more

Paper Surprising Perimeter
Find the perimeter of a folded sheet of A4 paper as described in this short video. more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.