
 |
Exam-Style Questions on SequencesProblems on Sequences adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
The first five terms of an arithmetic sequence are:
$$-20, -17, -14, -11, -8$$Find an expression for the \(n^{th}\) term of the sequence.
2. | GCSE Higher |
Here is a picture of four models. Some of the cubes are hidden behind other cubes.

Model one consists of one cube. Model two consists of four cubes and so on.
(a) How many cubes are in the third model?
(b) How many cubes are in the fourth model?
(c) If a fifth model were built, how many cubes would it take?
(d) Find an expression for the number of cubes used in the nth model.
(e) Sketch a side view, front view and plan view of the fourth model.
3. | GCSE Higher |
In a sequence
$$T_1 = 19,\quad T_2 = 13,\quad T_3 = 7,\quad T_4 = 1.$$
Find
(a) \(T_5\)
(b) \(T_n\).
(c) \(T_{50}\)
4. | GCSE Higher |
(a) Find the \(n\)th term of the sequence 7, 13, 19, 25,...
(b) In a sequence of four numbers, the difference between each number is 9.
The sum of the four numbers is 2.
What are the numbers in the sequence?
You must show all your working.
5. | GCSE Higher |
Work out an expression for the nth term of the quadratic sequence
$$0,9,22,39,60, ...$$Give your answer in the form \(an^2 + bn + c\) where a, b and c are constants.
6. | GCSE Higher |
Find an expression, in terms of \(n\), for the \(n\)th term of the sequence that has the following first five terms:
$$6 \qquad 13 \qquad 23 \qquad 36 \qquad 52 $$7. | IGCSE Extended |
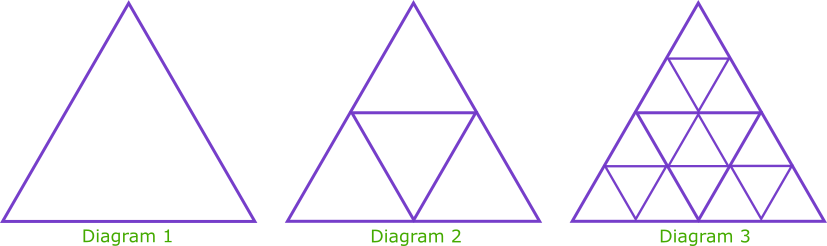
The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre.
In the second diagram there are four triangles each with sides of length \(\frac{1}{2}\) metre.
In the third diagram there are 16 triangles each with sides of length \(\frac{1}{4}\) metre.
(a) Complete this table for more diagrams.
| Diagram 1 | Diagram 2 | Diagram 3 | Diagram 4 | Diagram 5 | Diagram 6 | Diagram \(n\) | ||
| Length of Side | 1 | \(\frac{1}{2}\) | \(\frac{1}{4}\) | |||||
| Power of 2 | 20 | 2-1 | 2-2 |
(b) Complete this table for the number of the smallest triangles in diagrams 4, 5 and 6.
| Diagram 1 | Diagram 2 | Diagram 3 | Diagram 4 | Diagram 5 | Diagram 6 | Diagram \(n\) | ||
| Number of smallest triangles | 1 | 4 | 16 | |||||
| Power of 2 | 20 | 22 | 24 |
(c) Calculate the number of the smallest triangles in the diagram where the smallest triangles have sides of length \(\frac{1}{256}\) metre.
8. | GCSE Higher |
The diagrams below show a sequence of patterns made from red and yellow tiles.

(a) Find an ex
The total number of red and yellow tiles in each pattern is always the sum of the squares of two consecutive whole numbers.
(b) Find an ex
(c) Is there a pattern for which the total number of tiles is 303? Give a reason for your answer.
(d) Explain why the total number of tiles in any pattern of this sequence is always an odd number.
9. | IB Standard |
The first three and last terms of an arithmetic sequence are \(7,13,19,...,1357\)
(a) Find the common difference.
(b) Find the number of terms in the sequence.
(c) What is the sum of the sequence.
10. | IB Standard |
An arithmetic sequence is given by 6, 13, 20, …
(a) Write down the value of the common difference, d.
(b) Find \(u_{100}\);
(c) Find \(S_{100}\);
(d) Given that \(u_n=1434\) , find the value of n.
11. | IB Standard |
In an arithmetic sequence, the fifth term is 44 and the ninth term is 80.
(a) Find the common difference.
(b) Find the first term.
(c) Find the sum of the first 50 terms of the sequence.
12. | IB Standard |
A square is drawn with sides of length 32 cm. The midpoints of the sides of this square are joined to form a new square and four red triangles. The process is repeated to produce yellow triangles and then again to produce blue triangles.

The length of the equal sides of the red triangles are denoted by \(x_1\) and their areas are each \(A_1\).
The length of the equal sides of the yellow triangles are denoted by \(x_2\) and their areas are each \(A_2\).
The length of the equal sides of the blue triangles are denoted by \(x_3\) and their areas are each \(A_3\).
(a) The following table gives the values of \(x_n\) and \(A_n\), for \(1\le n\le3\). Copy and complete the table.
| \(n\) | 1 | 2 | 3 |
| \(x_n\) | 16 | ||
| \(A_n\) | 128 |
(b) The process of drawing smaller and smaller squares inside each new square is repeated. Find \(A_7\)
(c) Consider an initial square of side length \(k\) cm. The process described above is repeated indefinitely. The total area of one of each colour triangles is \(k\) cm2. Find the value of \(k\).
13. | IB Applications and Interpretation |
A celebrity football match is planned to take place in a large stadium.

The most expensive tickets are in the first row. The ticket price for each row forms an arithmetic sequence. Prices for the first four rows are shown in the following table.
| Row number: | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Price per seat | £50 | £48.50 | £47 | £45.50 |
(a) Write down the value of the common difference, \(d\).
(b) Calculate the price of a ticket in the 19th row.
(c) Find the total cost of buying 5 tickets in each of the first 10 rows.
14. | IB Analysis and Approaches |
An arithmetic sequence has first term 99 and common difference \(-5.5\).
(a) Given that the \(k\)th term of the sequence is zero, find the value of \(k\).
Let \(S_n\) denote the sum of the first \(n\) terms of the sequence.
(b) Find the maximum value of \(S_n\).
15. | IB Standard |
The first term of an infinite geometric sequence is 10. The sum of the infinite sequence is 500.
(a) Find the common ratio.
(b) Find the sum of the first 9 terms.
(c) Find the least value of n for which Sn > 250.
16. | IB Studies |
A Grecian amphitheatre was built in the form of a horseshoe and has 22 rows.
The number of seats in each row increase by a fixed amount, \(d\), compared to the number of seats in the previous row. The number of seats in the fifth row, \(u_5\), is 58, and the number of seats in the ninth row, \(u_{9}\), is 86. \(u_1\) represents the number of seats in the first row.
(a) Write an equation for \(u_5\) in terms of \(d\) and \(u_1\).
(b) Write an equation for \(u_{9}\) in terms of \(d\) and \(u_1\).
(c) Write down the value of \(d\);
(d) Write down the value of \(u_1\).
(e) Find the total number of seats in the amphitheatre.
Some time later, a second level was added to increase the amphitheatre’s capacity by another 2590 seats. Each row has five more seats than the previous row. The first row on this level has 82 seats.
(f) Find the number of rows on the second level of the amphitheatre.
17. | IB Analysis and Approaches |
Consider an arithmetic sequence where \(u_{10}=S_{10}=15\). Find the value of the first term, \(u_1\) and the value of the common difference, \(d\).
18. | A-Level |
In a geometric series the common ratio is \(r\) and sum to \(n\) terms is \(S_n\).
Given that \(S_4 = \frac{8}{9} S_{\infty} \) and \(r = \pm \frac{1}{\sqrt{k}} \) find the value of \(k\).
19. | IB Analysis and Approaches |
Consider a geometric sequence with first term 2 and common ratio 9.
\(S_n\) is the sum of the first \(n\) terms of the sequence.
(a) Find an expression for \(S_n\) in the form \(\frac{a^n - 1}{b}\), where \(a, b \in \mathbb{Z}^+\).
(b) Hence, show that \(S_1 + S_2 + S_3 + \cdots + S_n = \dfrac{9^{n+1} - 9 - 8n}{32}\).
20. | IB Studies |
Chris checks his Twitter account and notices that he received a tweet at 8:00am. At 8:05am he forwards the tweet to four people. Five minutes later, those four people each forward the tweet to four new people. Assume this pattern continues and each time the tweet is sent to people who have not received it before.
The number of new people who receive the tweet forms a geometric sequence:
$$1 , 4 , …$$(a) Write down the next two terms of this geometric sequence.
(b) Write down the common ratio of this geometric sequence.
(c) Calculate the number of people who will receive the tweet at 8:40am.
(d) Calculate the total number of people who will have received the tweet by 8:40am.
(e) Calculate the exact time at which a total of 5 592 405 people will have received the tweet.
21. | IB Analysis and Approaches |
The sum of the first n terms of a geometric sequence is given by:
$$S_n = \sum_{r=1}^{n} \dfrac{3}{4}\left( \dfrac{5}{7} \right) ^r $$(a) Find the first term of the sequence, \(u_1\).
(b) Find \(S_\infty\).
(c) Find the least value of \(n\) such that \(S_\infty - S_n < 0.001\).
22. | IB Analysis and Approaches |
Consider the arithmetic sequence \( u_1, u_2, u_3, \ldots \).
The sum of the first \( n \) terms of this sequence is given by \( S_n = 2n^2 + n \).
(a) Find the sum of the first six terms.
(b) Given that \( S_7 = 105 \), find \( u_7 \).
(c) Find \( u_1 \).
(d) Hence or otherwise, write an expression for \( u_n \) in terms of \( n \).
Consider a geometric sequence, \( v_n \), where \( v_2 = u_1 \) and \( v_4 = u_7 \).
(e) Find the possible values of the common ratio, \( r \).
(f) Given that \( v_{30} < 0 \), find the value of \( v_5 \).
23. | IB Standard |
The sums of the terms of a sequence are given as follows where \(k\in \mathbb{Z}\):
$$S_1=k+1, S_2=4k+3, S_3=9k+7, S_4=16k+15$$(a) Find the first four terms of the sequence.
(b) Find a general ex
24. | IB Studies |
Consider the number sequence where \(u_1=500, u_2=519, u_3=538\) and \(u_4=557\) etc.
(a) Find the value of \(u_{30}\)
(b) Find the sum of the first 12 terms of the sequence:
$$\sum_{n=1}^{12} u_n $$Another number sequence is defined where \(w_1=4, w_2=8, w_3=16\) and \(w_4=32\) etc.
(c) Find the exact value of \(w_{10}\).
(d) Find the sum of the first 9 terms of this sequence.
\(k\) is the smallest value of \(n\) for which \(w_n\) is greater than \(u_n\).
(e) Calculate the value of \(k\).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.