
 |
Exam-Style Questions on AlgebraProblems on Algebra adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher [263] |
Solve the following linear equations showing clearly each step of your working.
(a) \( \frac{6}{x} = 24 \).
(b) \(11x - 5 = 9(x + 9) \).
2. | GCSE Higher [261] |
The diagram shows an isosceles triangle (not drawn to scale).

Angle ABC = angle ACB, AB = \(3x+8\) and AC = \(5x-7\).
Use an algebraic method to find the value of \(x\).
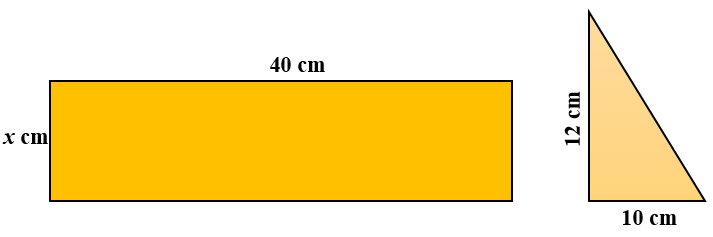
3. | GCSE Foundation [333] |
The diagrams show a triangle and a rectangle (not drawn to scale).
The area of the rectangle is six times larger than the area of the triangle. Find the value of \( x \)
4. | GCSE Higher [164] |
The perimeter of the triangle is the same length as the perimeter of the square.
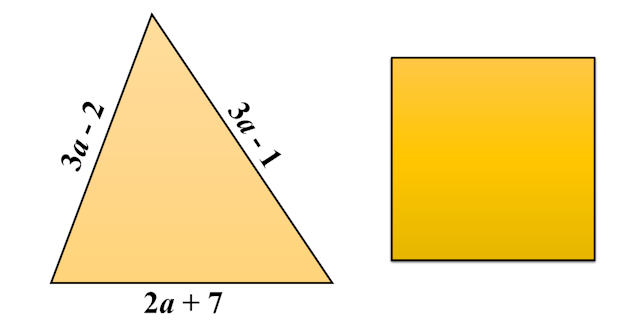
Find an ex
6. | GCSE Higher [143] |
Aimee, Natasha and Ruby play hockey.
If altogether they have scored 35 goals, how many goals did they each score?
7. | GCSE Higher [719] |
Julie is on holiday and buys some fruit from the local market.
She buys \(x\) mangos, \((x+4)\) guavas and \((3x-5)\) bananas.

The total number of pieces of fruit Julie buys is 29.
(a) Find the number of mangos Julie buys.
(b) The cost of one mango is 35 baht.
The cost of one guava is 18 baht.
If the total cost of all the fruit is 455 baht, find the cost, in baht, of one banana.
(c) What is the equivalent cost of the fruit Julie has bought in British pounds if the exchange rate with Thai baht is currently:
£1 = 46 baht.
8. | GCSE Higher [638] |
(a) Simplify:
$$ p^6 \times p^3$$(b) Simplify:
$$ \dfrac{a^5b^7}{a^4b} $$(c) Solve:
$$ \dfrac{2w}{9} \gt 10$$9. | GCSE Higher [188] |
Luke, Leia and Han swim lengths of a swimming pool to raise money for charity.

How many lengths did each person swim?
10. | GCSE Higher [243] |
Simplify then find the square root of this expression:
$$\frac{y}{(1-y)^2} - \frac{y}{1-y}$$11. | GCSE Higher [545] |
(a) The expression \( (x+1)(2x-3)(3x+4) \) can be written in the form \(ax^3 + bx^2 + cx + d \) where \(a, b, c\) and \(d\) are integers. Find the values of \(a, b, c\) and \(d\).
(b) Solve the following inequality:
$$(x-2)^2 \lt \frac{16}{49}$$12. | GCSE Higher [331] |
Two rectangles, not drawn to scale, are shown below. All measurements are in centimetres. Both rectangles have the same areas. Work out the perimeter of the rectangle on the left.
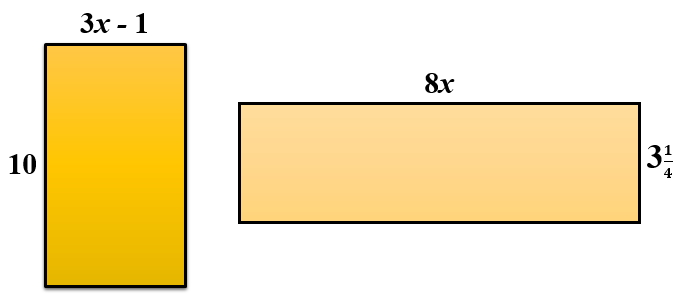
13. | GCSE Higher [332] |
The area of rectangle PQRS (not to scale) is 80cm2.
(a) Show that \( x^2 + 14x = 40\).
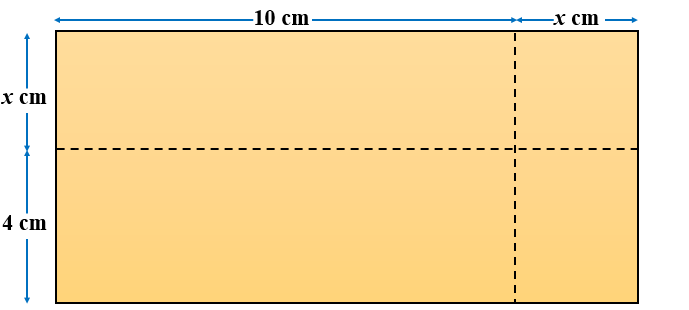
(b) Find the value of \( x \) giving your answer correct to three significant figures.
14. | GCSE Higher [386] |
Expand and simplify the following expression:
$$ (2x^2 + 3)(4x - 5) - 8x(x^2 - 7) $$15. | GCSE Higher [662] |
(a) Express the following as a single fraction in its simplest form.
$$ \dfrac{6}{x-3} - \dfrac{2}{x-1} $$(b) Expand and simplify the following:
$$ (x+ 2)(3x-5)(5x+1) $$16. | GCSE Higher [181] |
Show that you understand equations and inequalities by answering the following:
(a) Solve \(5x^2=80\)
(b) Solve \(8x + 2 \gt x + 7\)
(c) Write down the largest integer that satisfies \(8x - 2 \lt 25\)
(d) Solve the following pair of equations
$$3x + 5y = 21$$ $$8x - 5y = 1$$17. | GCSE Higher [702] |
(a) Simplify \( 6(3a-2)-2(a-3) \)
(b) Simplify \( \frac{3x}{4} - \frac{2x}{3} \)
(c) Rearrange the formula to make m the subject:
$$ w = \frac{m+n}{3-m} + 7 $$(d) Solve \( x^8 = 5600 \)
(e) Solve \( |x+5| = 9 \)
(f) Solve by factorising:
$$ 9z^2 - 27z + 20 = 0 $$18. | GCSE Higher [742] |
A red square has sides of length \(x\) cm. A blue rectangle has sides of length \(3x-1\) cm and \(x-2\) cm. The diagrams below are not drawn to scale.
The area of the rectangle is \(132\) cm2 greater than the area of the square.
The difference between the perimeters of the two shapes is \(p\) cm.
Find the value of \(p\).
You must show all your working.
19. | IGCSE Extended [238] |
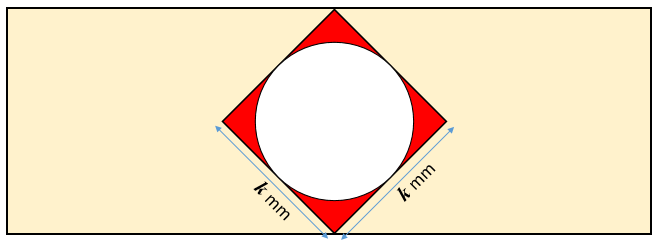
A circle is drawn inside a square so that it touches all four sides of the square.
(a) If the sides of the square are each \(k\) mm in length and the area of the red shaded region is \(A\) mm2 show that:
$$4A=4k^2-\pi k^2$$(b) Make \(k\) the subject of the formula \(4A=4k^2-\pi k^2\)
20. | GCSE Higher [240] |
One is added to the product of two consecutive positive even numbers. Show that the result is a square number.
21. | GCSE Higher [276] |
(a) Simplify the following expression.
$$ \frac{x^2 - 4}{3x^2 + 13x + 14}$$(b) Make b the subject of the following formula.
$$ a = \frac{7(3b-c)}{b}$$22. | GCSE Higher [129] |
Rätselzeit school has an annual sports day in which the mathematics teachers are in charge of the scoring system.
The points scored for throwing the discus are worked out using the formula:
$$p = 15(d – 4.2)$$where \(p\) is the number of points scored when the discus is thrown a distance of \(d\) metres.
(a) How many points does Homer score for throwing the discus a distance of 52 metres?
(b) How far did Marge throw the discus if she scored 492 points?
The points scored for running 400 metres are worked out using the formula:
$$p = 6(95 – t)^2$$where \(p\) is the number of points scored when the time taken is \(t\) seconds.
(c) Lisa scores 1014 points for the 400 metres race. Work out the time, in seconds, it took Lisa.
The formula for the number of points scored in the 400 metres race should not be used for \(t\gt n\).
(d) State the value of \(n\) giving a reason for your answer.
23. | GCSE Higher [683] |
(a) Find the ratio \(a:b \) given the equation:
$$ 7a + 2b = 4(a+b) $$(b) Find the ratio \( c:d \) given the following equation where \( c \gt 0 \text{ and } d \gt 0 \).
$$ 2c^2 = 5cd - \dfrac{25d^2}{8} $$24. | GCSE Higher [175] |
Betsy thinks that \((3x)^2\) is always greater than or equal to \(3x\).
Is she is correct?
Show your working to justify your decision
26. | GCSE Higher [500] |
Given that:
$$ x^2 : (5x + 3) = 1 : 3 $$find the possible values of \(x\).
27. | GCSE Higher [521] |
Show that:
$$3 - (4x^2+11x+7) \div (x^2+4x+3) $$simplifies to \( \frac{a-x}{x+b}\) where \(a\) and \(b\) are integers.
28. | GCSE Higher [299] |
The expression below can be written as a single fraction in the form \( \dfrac{a-bx}{x^2-25} \) where \(a\) and \(b\) are integers.
$$ \frac{x-4}{x-5} - 2 + \frac{x+1}{x+5}$$Work out the value of \(a\) and the value of \(b\).
29. | GCSE Higher [196] |
If \(y = 5x^4 + 3x^2\) and \(x=\sqrt{w+2}\), find \(w\) when \(y = 12\) showing each step of your working.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.