
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
The diagram shows a water tank in the shape of a cylinder. It has a diameter of 76cm anf a height of 36cm.
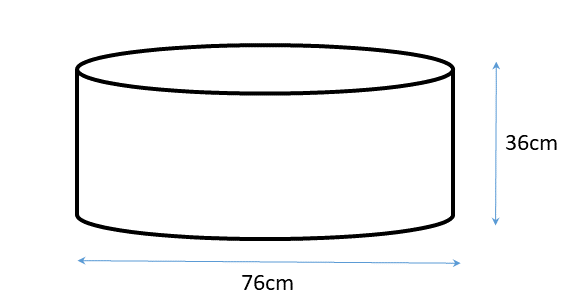
It is filled at the rate of 0.3 litres per minute. How long does it take to completely fill the tank?
[1 litre = 1000 cm3]
2. | GCSE Higher |
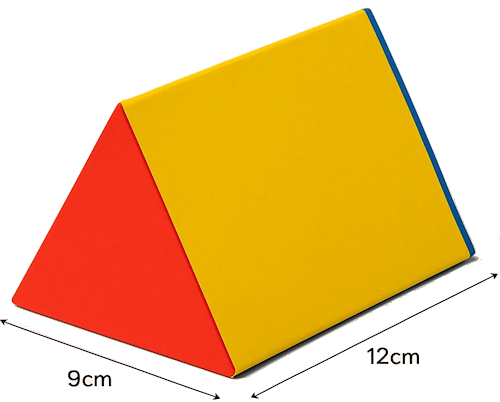
The cross-section of a prism is an equilateral triangle of side 9cm. The length of the prism is 12 cm.
Calculate the total surface area of the prism.
3. | GCSE Higher |
An ornamental lake is in the shape of a semicircle with a diameter of 900 metres.
(a) Calculate the perimeter of the lake to the nearest metre.
(b) The lake has a uniform depth of 1.5 metres. Calculate the volume of the water in the lake in cubic metres to the nearest integer.
(c) Give the volume of the lake in litres. Give your answer correct to three significant figures in standard form.

4. | GCSE Higher |
Babatunde has to paint four containers.
Each container is in the shape of a cylinder with a diameter of 1.2m and a length of 3.2m.
How many tins of paint will Babatunde need to buy to completely cover each of the four containers if each tin of paint covers 6m2?
You must show all of your working.

[The surface area of a cylinder of radius \(r\) and height (or length) \(h\) is \(2\pi rh + 2\pi r^2\)]
5. | GCSE Higher |
The diagram show a solid cone painted two different colours.
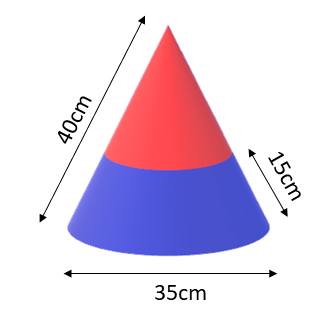
Find the area of the curved surface of a cone with a base diameter of 35cm and slant height of 40cm that is painted blue, below a circle drawn at a slant height of 15cm above the base.
Give your answer to three significant figures and show your working.
6. | GCSE Higher |
A builder needs to lift a steel block. It is a cuboid with dimensions 2 m by 0.2 m by 0.2 m. Steel has a density of 7.6 g/cm3.
The builder's lifting gear can lift a maximum load of 500 kg. Can the lifting gear be used to lift the steel block?
Justify your decision.
7. | GCSE Higher |
A solid steel cylinder with a cylindrical hole running through its centre contains \(2800 \, \text{cm}^3\) of steel. The overall radius of the object is \(10 \, \text{cm}\), and the radius of the cylindrical hole is \(5 \, \text{cm}\).

(a) Calculate the length of the object.
(b) The solid steel used in the object is melted and moulded into spheres, each with a radius of \(1 \, \text{cm}\).
How many spheres will be produced?
8. | IGCSE Extended |
[The surface area of a sphere of radius \(r\) is \(4\pi r^2\) and the volume is \(\frac43\pi r^3\)]
A solid metal sphere has a radius of 7.5 cm.
(a) Calculate the volume of the sphere to the nearest cubic centimetre.
(b) Calculate the surface area of the sphere to the nearest square centimetre.
(c) If one cubic centimetre of the metal has a mass of 4.9 grams calculate the mass of the sphere to three significant figures.
(d) Two of these spheres are placed in the water in a cylindrical tank with base diameter 32cm. Before they were lowered in the depth of the water was 19cm. Calculate the new depth of water in the cylinder when the spheres are fully submerged.
9. | GCSE Higher |
A circular dart board has radius of 30 cm.
(a) Calculate the area of the front face of the dart board in cm2, giving your answer as a multiple of \(\pi\).
(b) The volume of the dart board is 4500\(\pi\) cm3. Calculate the thickness of the dart board.
10. | GCSE Higher |
The diagram, not drawn to scale, shows the plan for a large, three dimensional sign which has been ordered to hang outside an ice cream shop.
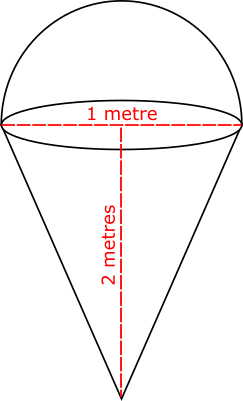
The sign is made of a hemisphere on top of a right cone.
The height of the cone is 2 m.
The top of the cone has a diameter of 1 m.
The hemisphere has a diameter of 1 m.
The total volume of the shape is \(k \pi \) cm3, where \(k\) is an integer.
Work out the value of k.
Where \(r\) is the radius of the sphere.
$$ \text{Volume of a cone} = \frac{\pi r^2 h}{3} $$Where \(r\) is the radius of the circular end of the cone and \(h\) is the height of the cone.
11. | GCSE Higher |
The illustration shows a greenhouse in the shape of a pentagonal prism. The front of the greenhouse is a pentagon with a single line of symmetry. The sides of the greenhouse are vertical.
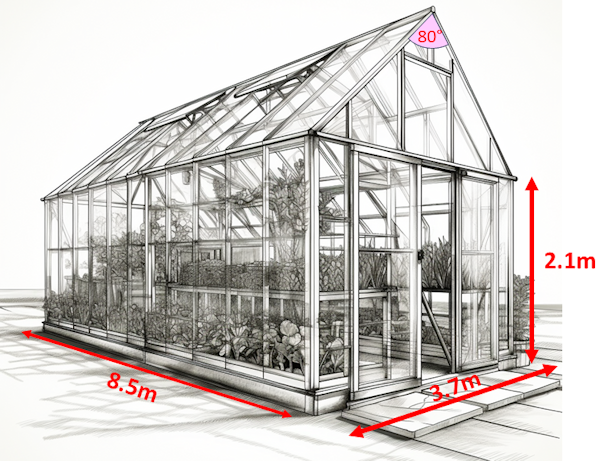
Find the volume of the greenhouse in cubic metres correct to the nearest integer.
12. | IB Studies |
Twenty four spherical shaped chocolates are arranged in a box in four rows and six columns.

Each chocolate has a radius of 1.2 cm.
(a) Find the volume of one chocolate.
(b) Write down the volume of 24 chocolates.
The 24 chocolates fit perfectly in the box with each chocolate touching the ones around it or the sides of the box.
(c) Calculate the volume of the box.
(d) Calculate the volume of empty space in the box.
(e) What percentage of the contents of the box is chocolate?
13. | IGCSE Extended |
The three sides of an equilateral triangle are tangents to a circle of radius \(r\) cm. The sides of the triangle are each 10cm long.

(a) Calculate the value of \(r\).
The second diagram shows a box in the shape of a triangular prism of length 15cm.

The cross section is an equilateral triangle with sides of length 10cm.
(b) Calculate the volume of the box.
The box contains cookies. Each cookie is a cylinder of radius 2.8cm and height 5mm.
(c) Calculate the largest number of cookies that will fit in the box.
(d) Calculate the volume of one cookie in cubic centimetres.
(e) Calculate the percentage of the volume of the box not filled with cookies.
14. | GCSE Higher |
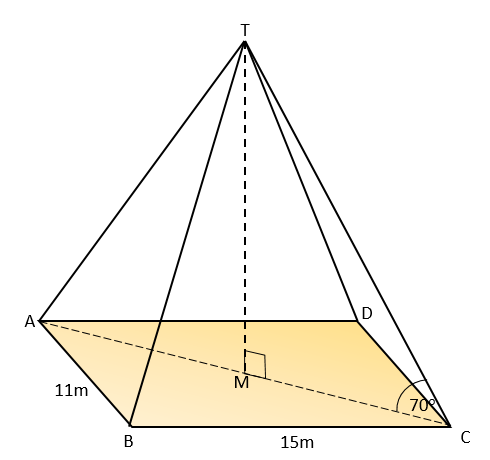
The diagram shows a rectangular-based pyramid, TABCD (not drawn to scale).
The horizontal base ABCD has sides of lengths 11m and 15m. The centre of the base of the pyramid is M.
Angle TMC is 90° and angle TCM is 70°
The volume of a pyramid is \( \frac13 \) × area of base × perpendicular height. Calculate the volume of this pyramid.
15. | GCSE Higher |
The photograph shows a horizontal container for water with a uniform cross-section.
The cross-section is a semicircle.

The radius of the semicircle is 65cm and the length of the container is 3m.
(a) Calculate the volume of water in the container when full.
Yesterday the container was partially filled with water. The greatest depth of the water in the container was 50cm.
(b) Calculate the number of litres of water in the container giving your answer correct to the nearest integer.
16. | GCSE Higher |
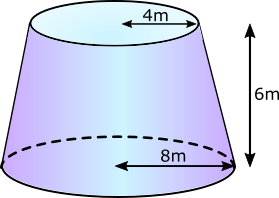
The volume of a cone can be calculated using the formula \(V=\frac13 \pi r^2 h \) and the area of the curved surface of a cone can be calculated using \(A= \pi r l\) (where \(r\) is the radius and \(l\) is the slant height).
(a) Calculate the volume of this frustum;
(b) Calculate the total surface area of this frustum.
17. | GCSE Higher |
The diagram shows a water tank in the shape of a trapezoidal prism.
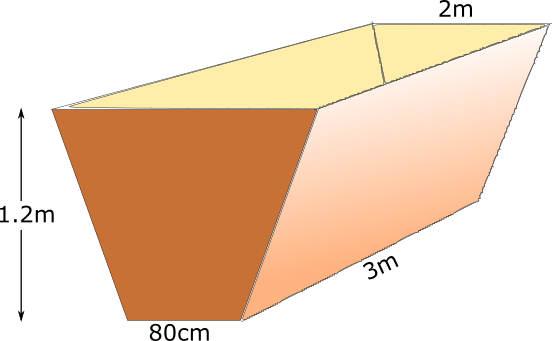
Winthrop begins filling the tank with a hose pipe. After 30 minutes there are 900 litres of water in the tank. How many more minutes will it take until the tank is half full? ( \( 1m^3 = 1000 \) litres )
18. | IB Analysis and Approaches |
A metal sphere has a radius 7.2 cm.
(a) Find the volume of the sphere giving your answer in standard form.
The sphere is to be melted down and remoulded into the shape of a square-based pyramid with a height of 10.3 cm.
(b) Find the length of one side of the pyramid's square base to the nearest millimetre.
19. | IB Studies |
A solid metal cylinder has a base radius of 5cm and a height of 9cm.
(a) Find the area of the base of the cylinder.
(b) Find the volume of the metal used in the cylinder.
(c) Find the total surface area of the cylinder.
The cylinder was melted and recast into a solid cone with a circular base radius, OB (where O is the centre of the circle), of 7cm. The vertex of the cone is the point C.
(d) Find the height, OC, of the cone.
(e) Find the size of angle BCO.
(f) Find the slant height, CB.
(g) Find the total surface area of the cone.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.