Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for October 2025, a month that begins with a package of poetry and ends with a Halloween haunting. Before I tell you more about those events, let's go on a little journey to Saint Bees.

As I was going to Saint Bees
I passed a wood that had N trees
Each tree had N birds’ nests
And in each nest, N eggs rest
Now in this wood there lived a snake
And N eggs for breakfast it did take
Six children wished to save the rest
By guarding eggs in every nest
They divided the number of eggs remaining
By six (using their primary school training)
Can you calculate with exact precision
What’s the remainder of this division?
If you get an answer, I'd love to hear how you or your students solved the puzzle. Fire off an email to gro.musnarT@rettelsweN
While you think about that, here are some of the key resources added to the Transum website during the last month.
Matrix Multiplier. They're not on every syllabus but matrices do raise their heads here and there. Prompted by a puzzle in Chris Smith's wonderful newsletter one Saturday morning I decided that it wouldn't hurt if Transum had a matrix multiplication calculator on the website. So now it does! But I didn't stop there. There's a related exercise too, called Matrix Multiplication.
Mystery Numbers has been swirling around my head since the 1980s. The clues are given in the form of abbreviations, and your task is to write out the full phrase. Some of the clues are UK-biased, but you only need to solve 15 out of 20 to earn a trophy. Not only is it a great activity to use with students, it has also proved very popular as a handout at parents’ evenings and similar events.
There is no end of great maths ideas in Chris's newsletter (https://x.com/aap03102). An edition earlier last month prompted me to share a method for finding the cube roots of large numbers. It is predictably called Cube Root Trick. Thanks to Chris and a Chelsea FC striker.
Emergency Lessons are something I hope you’ll never need. They are quick, adaptable plans for a wide range of abilities, each focused on a different section of the maths curriculum. Keep them up your sleeve, just in case!

Halloween haunts the world at the end of this month, and of course there are a number of mathematically linked activities here on Transum. There’s the 31 October Starter, a true-false activity called Trick or Treat, a proportion activity called Double, Double, Halve and Treble, a puzzle called Squorder, and, from a previous newsletter, the Pumpkin Price puzzle.
🎃 🎃 🎃
There’s only one thing I don’t like about Halloween… which is …
I am aware that it is not just the Starters that are projected onto the whiteboard for the whole class to see. Many of the interactive exercises are also projected so that students can see the questions even if they don't have their own internet-connected device. In the middle of last month, some buttons were added for subscribers to help them better display exercises and answers.

National Poetry Day in the UK takes place annually on the first Thursday in October. The Maths Poems page contains links to topic-specific poems I have written and collected over the years. Please let me know of any rhyming verses that you know of that help memorise specific mathematical concepts. You could even make one up yourself and before you know it, you've become a poet!
Recently I’ve added some large images to Topic pages. Some illustrate key ideas, others are light-hearted prompts. The jokes are purposeful: they encourage students to think about the underlying concept before understanding the humour. The image on the Pythagoras page is a discussion starter and could lead into exploring areas of similar shapes on the sides of a right-angled triangle. I haven’t tried it with students yet, so let me know if you do.
For future reference, there is a 'mirror' site that contains all the Transum Starters and activities. It is at www.transum.info The only difference is that it doesn't contain the details of your Transum subscription account, so you won’t be able to log in there. If it happens that for some reason Transum.org goes offline, you can use the mirror site until the main site is restored.
Finally, the answer to last month's puzzle which was:
Farmers A and B have 30 cows between them and sell at different prices, each receiving the same amount. If A had sold at B’s price he would have received £320, and if B had sold at A’s price she would have received £245. How many cows did Farmer A own?
The answer is 16. You can see some creative solution methods below from some wonderful members of the Transum community. Thanks so much.
This puzzle is adapted from Elementary Algebra for Schools by H. S. Hall and S. R. Knight, published in 1885.
That's all for now,
John
P.S. I always thought my Maths teacher was spooky. Last Halloween he said, "Look at the screen and I'll go through it again"!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Mala, New Zealand
Monday, September 1, 2025
"Let x = number of cows farmer A had. Then farmer B would have had 30-x cows.
Let y = farmer A’s selling price for each cow and let p= farmer B’s selling price for each cow.
Then, xy =p(30-x)…….they get the same money for their cows…equation 1
Also, px = 320 which implies that p= 320/x……eqn 2
And y(30-x) = 245 which implies that y= 245/(30-x)…eqn 3
Substituting values of p and y from equations 2 and 3 into equation 1 and simplifying, we get
x^2 -256x +3840 = 0 which gives x = 240 or 16. Since x is less than 30, x = 16. Farmer A owned 16 cows. "
Kevin, Australia
Monday, September 1, 2025
"Farmer A owned 16 cows and sold the cows for 17.50 pounds each.
Farmer B owned 14 cows and sold the cows for 20 pounds each. 🐮 🐮 🐮 "
Chris, Scotland
Monday, September 1, 2025
"Pleased that the 1885 puzzle was within my grasp!
Farmer A has a cows, selling each for £x.
Farmer B then has (30-a) cows, selling each for £y.
Three facts:
Equal income: ax = (30-a)y
Switch price and Farmer A earns 320: ay = 320
Switch price and Farmer B earns 245: x(30-a) = 245
If we take these last two equations and rearrange then we get x and y in terms of a: y = 320/a and x = 245/(30-a)
Substituting these into the equal income equation we end up with 245a/(30-a) = 320(30-a)/a
This can be simplified to get a quadratic 75a^2 - 19200a + 288000 = 0
Dividing through by 75 we get a^2 - 256a + 3840 = 0
Factorise (a - 240)(a - 16) = 0
This gives two solutions: a = 240 or a = 16
But there were only 30 cows in the first place so Farmer A must've had 16 cows (selling each at £17.50) and Farmer B must've had 14 cows selling at £20.
Thanks. for the amoooosing puzzle. "
Rick, United States
Tuesday, September 2, 2025
"Here is my answer to the September 2025 puzzle. It appears to be four equations with four unknowns.
Let A = number of cows owned by farmer A.
Let B = number of cows owned by farmer B.
Let X = price of cows owned by farmer A.
Let Y = price of cows owned by farmer B.
[1] A+B=30
[2] AX=BY
[3] AY=320
[4] BX=245
From equation [3]
[5] Y=320/A
And from equation [4]
[6] X=245/B
Substituting the values for X and Y into equation [2]
[7] 245A/B=320B/A
From equation [1]
[8] B=30-A which can be incorporated into equation [7].
[9] 245A/(30-A)=320(30-!)/A)
Since I am lazy, I let CoPilot solve this and received two answers to the quadratic equation (16 and 240) but since 240 is not in the range of 1 to 30, the answer is 16 cows owned by A. "
Leonard, United States
Tuesday, September 2, 2025
"Here’s my take on September’s Puzzle of the Month.
 "
"
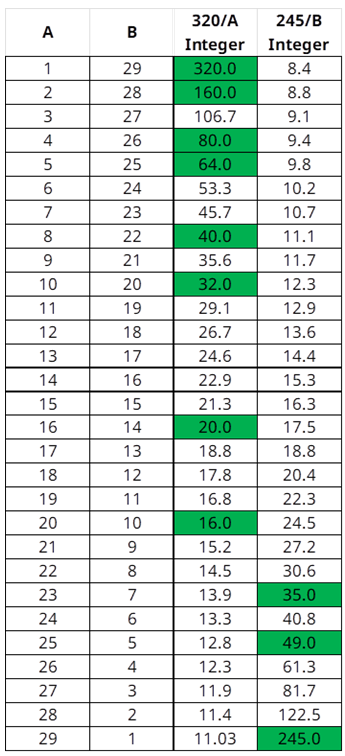
Focusing in on integer solutions, I considered the money received after swapping prices. Considering the prime factorizations of 320 (2,2,2,2,2,2,5) and 245 (5,7,7) respectively, I created the following table in MSExcel.
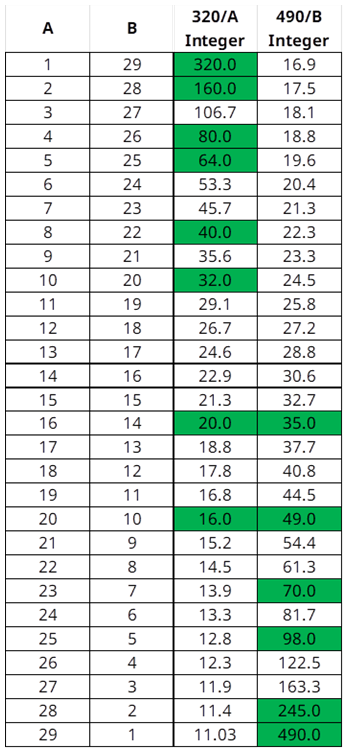
Unfortunately, none of the rows were solutions for both criteria. I took this to mean that the prices might not be integers (certainly the number of cows were). The easiest “path forward” seemed to be to add a factor of 2 to the 245 amount. The new table looked like this:
Further investigation of the (16,14) and (20,10) combinations showed the Farmer A having 16 cows was indeed a solution. Here is my final analysis: