Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
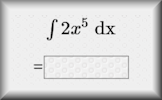Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions.
Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.
Here are some exam-style questions on this statement:
- "Find:" ... more
- "(a) Find \(\int (4x+5) dx\)." ... more
- "A particle moves in a straight line. During the first nine seconds the velocity, \(v\) ms-1 of the particle at time \(t\) seconds is given by:
$$ v(t) = t \cos(t+5) $$
The following diagram shows the graph of v:
" ... more - "Consider the region where \(0 \lt x \lt 2\pi \) and \(\sin{x} \gt \cos{2x} \)" ... more
- "The function \(f\) is defined by \(f(x) = 8 - 5 \sin{x} \), for \( x \ge 0 \)." ... more
- "A particle moves in a straight line such that its velocity, \(v\) ms-1, at time \(t\) seconds is given by:" ... more
- "The diagram shows part of the graph of \(f(x)=Ae^{kx}+2\)." ... more
- "Consider the graph of the function \(f(x)=x^2+2\)." ... more
- "Make a sketch of a graph showing the velocity (in \(ms^{-1}\)) against time of a particle travelling for six seconds according to the equation:" ... more
- "Find the value of \(a\) if \(\pi \lt a \lt 2\pi\) and:" ... more
- "This graph represents the function \(f:x\to a \cos x, a\in \mathbf N\)" ... more
- "Let \(f(x) = \frac{ln3x}{kx} \) where \( x \gt 0\) and \( k \in \mathbf Q^+ \)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Areas between curves
We want to find the area between the curves \( y = x^2 + x - 2 \) and \( y = x + 2 \). First, we need to find the points of intersection between the two curves.
We can do this by setting the two equations equal to each other and solving for \( x \):
\[ \begin{align*} x^2 + x - 2 &= x + 2 \\ x^2 &= 4 \\ (x - 2)(x + 2) &= 0. \end{align*} \]The solutions are \( x = 2 \) and \( x = -2 \), so the curves intersect at these points.
Next, we'll find the area between the curves by integrating the difference between the two functions over the interval from \(-2\) to \(2\)
\[ \begin{align*} \text{Area} &= \int_{-2}^{2} \left( x + 2 - (x^2 + x - 2) \right) \,dx \\ &= \int_{-2}^{2} \left( -x^2 + 4 \right) \,dx \\ &= \left[ - \frac{x^3}{3} + 4x \right]_{-2}^2\\ &=(-8/3+8)-(8/3-8)\\ &=10 \frac23 \text{ square units} \end{align*} \]This Finding Areas Under Curves video is from Revision Village and is aimed at students taking the IB Maths Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
