A Level Mathematics Syllabus Statement

Syllabus Content

Understand and work with arithmetic sequences and series, including the formulae for n^th term and the sum to n terms

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

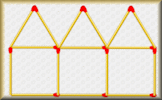Matchstick Patterns Create a formula to describe the nth term of a sequence by examining the structure of the diagrams.

Arithmetic Sequences An exercise on linear sequences including finding an expression for the nth term and the sum of n terms.

Arithmetic Sequences Video A reminder of how to find the next term, the nth term and the sum of terms of an arithmetic or linear sequence.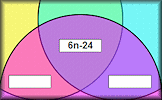

Venn Diagram of Sequences Find the formula for the nth term of sequences that belong in the given sets.

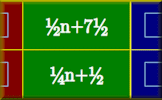Sequences Table Challenge Complete the table showing the terms of the sequences and the formulas for the nth terms.

Parts of Sequences Find the formula that describes the part of the sequence that can be seen

Here are some exam-style questions on this statement:

"(a) Find the $n$th term of the sequence 7, 13, 19, 25,..." ... more

"The first three and last terms of an arithmetic sequence are $7,13,19,...,1357$" ... more

"An arithmetic sequence is given by 6, 13, 20, …" ... more

"In an arithmetic sequence, the fifth term is 44 and the ninth term is 80." ... more

"A celebrity football match is planned to take place in a large stadium." ... more

"An arithmetic sequence has first term 99 and common difference $-5.5$." ... more

"A Grecian amphitheatre was built in the form of a horseshoe and has 22 rows." ... more

"Consider an arithmetic sequence where $u_{10}=S_{10}=15$. Find the value of the first term, $u_1$ and the value of the common difference, $d$." ... more

"Consider the arithmetic sequence $ u_1, u_2, u_3, \ldots $." ... more

See all these questions

Here is an Advanced Starter on this statement:

Same Series Sum
Find an arithmetic series and a geometric series that have the same sum of the first five terms. more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Sequences A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them. The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms. Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom. Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.

Featured Activity

The Transum Newsletter for May 2025 has just been published. Click on the image above to read about the latest developments on this site and try to solve the puzzle of the month. You can read the newsletter online or listen to it by downloading the podcast.

Prime Path Pace

The objective is to find a continuous path of prime numbers in the shortest time. So far this activity has been accessed 45 times and only 1 person has earned a Transum Trophy for completing it.

Furthermore

Arithmetic sequences and series are fundamental concepts in mathematics. An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. This difference is known as the common difference, denoted by $ d $.

The $ n^{th} $ term of an arithmetic sequence can be calculated using the formula:

$$ u_n = u_1 + (n - 1)d \\ \text{where } u_n \text{ is the } n^{th} \text{ term, } u_1 \text{ is the first term, and } d \text{ is the common difference.} $$

The sum of the first $ n $ terms ($ S_n $) of an arithmetic sequence can be found using the formula:

$$ S_n = \frac{n}{2}(2u_1 + (n - 1)d) \text{ or equivalently, } S_n = \frac{n}{2}(u_1 + u_n) \\ \text{where } S_n \text{ is the sum of the first } n \text{ terms.} $$

Sigma notation ($ \Sigma $) is a concise way to represent the sum of sequences. For an arithmetic sequence, it can be represented as:

$$ S_n = \sum_{r=1}^{n} (u_1 + (r - 1)d) $$

Example 1: Consider an arithmetic sequence where the first term $ u_1 = 5 $ and the common difference $ d = 3 $. Let's find the $ 10^{th} $ term and the sum of the first 10 terms.

Using the formula for the $ n^{th} $ term:

$$ u_{10} = 5 + (10 - 1) \cdot 3 = 32 $$

So, the $ 10^{th} $ term is 32.

Now, using the formula for the sum of the first $ n $ terms:

$$ S_{10} = \frac{10}{2}(2 \times 5 + (10 - 1) \cdot 3) = 185 $$

Thus, the sum of the first 10 terms of the given arithmetic sequence is 185.

Example 2: For an arithmetic sequence with the first term $ u_1 = 2 $ and the common difference $ d = 7 $, we can represent the sum of the first 6 terms using sigma notation as:

$$ S_6 = \sum_{r=1}^{6} (2 + (r - 1) \cdot 7) $$

This notation concisely represents the sum of the sequence: 2, 9, 16, 23, 30, and 37, which equals 117.

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.