Cookies are used on this website.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

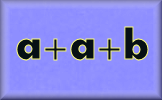• Algebraic Notation Simplification using the normal conventions of algebra.
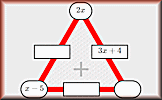• Algebragons Find the missing expressions in these partly completed algebraic arithmagon puzzles.
• Collecting Like Terms Video If you have forgotten what collecting like terms means watch this video for a quick refresher.
• Collecting Like Terms Practise your algebraic simplification skills with this self marking exercise.
• Brackets Levels 1 and 2 Learn how to remove brackets from simple algebraic expressions. This video is to help you do the online, self-marking exercise.
• Brackets Levels 3 to 5 Learn how to multiply the terms inside a pair of brackets by the term outside. This video is to help you do the online, self-marking exercise.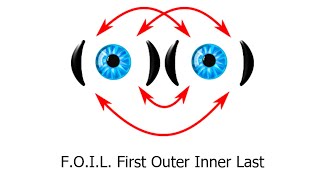
• Brackets Levels 6 to 8 Expand a pair of brackets using the clown's face method. This video is to help you do the online, self-marking exercise.
• Brackets Levels 9 and 10 The final video showing how algebraic expressions containing brackets can be simplified.
• Brackets Expand algebraic expressions containing brackets and simplify the resulting expression in this self marking exercise.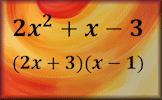
• Factorising Practise the skills of algebraic factorisation in this structured online self-marking exercise.
• Pascal's Triangle Get to know this famous number pattern with some revealing learning activities
• Algebraic Fractions A mixture of algebraic fraction calculations and simplifications.
• Polynomial Division Practise dividing one algebraic expression by another in this set of exercises.

Here are some exam-style questions on this statement:

• "Multiply out and simplify:" ... more
• "Find the highest common factor of the following two expressions:" ... more
• "Simplify then find the square root of this expression:" ... more
• "(a) Simplify \( \left(\dfrac{3a}{a^3 - 3}\right)^0 \)" ... more
• "(a) Simplify the following expression." ... more
• "Factorise the following expression" ... more
• "The expression below can be written as a single fraction in the form \( \dfrac{a-bx}{x^2-25} \) where \(a\) and \(b\) are integers." ... more
• "The function \(f\) is defined as \(f(x) = 12x^3 - 5x^2 -11x + 6 \)." ... more

See all these questions

Here is an Advanced Starter on this statement:

• Algebraic Product
  Finding the value of the expression is easier than you think! more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".