Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
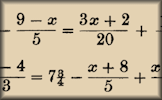Old Equations Solve these linear equations that appeared in a book called A Graduated Series of Exercises in Elementary Algebra by Rev George Farncomb Wright published in 1857.
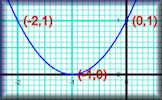Plotting Graphs Complete a table of values then plot the corresponding points to create a graph.
Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise.
New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations.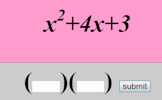
Factorising Quadratics An exercise about factorising quadratics presented one question at a time suitable for a whole class activity.
Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function.
Graph Patterns Find the equations which will produce the given patterns of graphs.
Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.
Human Graphs Students should be encouraged to stand up and make the shapes of the graphs with their arms.
Yes No Questions A game to determine the mathematical item by asking questions that can only be answered yes or no.
Here are some exam-style questions on this statement:
- "Write down the coordinates of the turning point on the graph of \(y = 9 - (x - 5)^2\)" ... more
- "The images below show a graphic display calculator screen with different functions displayed as graphs." ... more
- "Match the equation with the letter of its graph" ... more
- "The graph of the curve A with equation \(y=f(x)\) is transformed to give the graph of the curve B with equation \(y=5-f(x)\)." ... more
- "The graph of y = f(x) is drawn accurately on the grid." ... more
- "(a) By completing the square, solve \(x^2+8x+13=0\) giving your answer to three significant figures." ... more
- "The graph of the following equation is drawn and then reflected in the x-axis" ... more
- "The diagram below is a sketch of a curve, a parabola, which is not drawn to scale." ... more
- "Given that \(x^2 – 8x + 3 = (x – a)^2 – b\) for all values of x," ... more
- "(a) Find the interval for which \(x^2 - 9x + 18 \le 0\)" ... more
- "(a) Write \(2x^2+8x+27\) in the form \(a(x+b)^2+c\) where \(a\), \(b\), and \(c\) are integers, by 'completing the square'" ... more
- "Consider the function \(f(x)=\frac{1}{2}\left(2x-3\right)\left(x+5\right)\) for \(x \in \mathbb R\). The following diagram shows part of the graph of \(f\)." ... more
- "A function is defined as \(f(x) = 2{(x - 3)^2} - 5\) ." ... more
- "\(f\) and \(g\) are two functions such that \(g(x)=3f(x+2)+7\)." ... more
- "Let \(f(x)=5x^2-20x+k\). The equation \(f(x)=0\) has two equal roots." ... more
- "The graphs of the functions \(f(x)\), a parabola, and \(g(x)\), a straight line, meet at exactly one point." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
Furthermore
This video on Factorising Quadratic Functions and Equations is from Revision Village and is aimed at students taking the IB Maths AA Standard level course.
This video on Completing The Square is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
This video on Discriminant Test (Quadratics) is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
