Representing solutions of equations and inequalities
Term 1 starting in week 7 :: Estimated time: 3 weeks
- Understand the meaning of a solution
- Form and solve one-step and two-step equations (review)
- Form and solve one-step and two-step inequalities (review)
- Show solutions to inequalities on a number line
- Interpret representations on number lines as inequalities
- Draw straight line graphs (review)
- Find solutions to equations using straight line graphs
- Form and solve equations with unknowns on both sides
- Form and solve inequalities with unknowns on both sides
- Form and solve more complex equations and inequalities
For higher-attaining pupils:
- Represent solutions to inequalities using set notation
- Represent solutions to single inequalities on a graph
- Represent solutions to multiple inequalities on a graph
- Solve quadratic equations by factorisation
- Solve quadratic inequalities in one variable
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
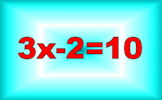 Equations A series of exercises, in increasing order of difficulty, requiring you to solve linear equations. The exercises are self marking.
Equations A series of exercises, in increasing order of difficulty, requiring you to solve linear equations. The exercises are self marking. eQuation Generator An unlimited supply of linear equations just waiting to be solved. Project for the whole class to see then insert the working in your own style.
eQuation Generator An unlimited supply of linear equations just waiting to be solved. Project for the whole class to see then insert the working in your own style. Nevertheless Players decide where to place the cards to make an equation with the largest possible solution.
Nevertheless Players decide where to place the cards to make an equation with the largest possible solution.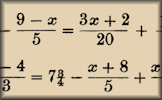 Old Equations Solve these linear equations that appeared in a book called A Graduated Series of Exercises in Elementary Algebra by Rev George Farncomb Wright published in 1857.
Old Equations Solve these linear equations that appeared in a book called A Graduated Series of Exercises in Elementary Algebra by Rev George Farncomb Wright published in 1857.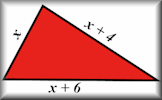 Algebraic Perimeters Questions about the perimeters and areas of polygons given as algebraic expressions.
Algebraic Perimeters Questions about the perimeters and areas of polygons given as algebraic expressions. Missing Lengths Find the unknown lengths in the given diagrams and learn some algebra at the same time.
Missing Lengths Find the unknown lengths in the given diagrams and learn some algebra at the same time. Algebra In Action Real life problems adapted from an old Mathematics textbook which can be solved using algebra.
Algebra In Action Real life problems adapted from an old Mathematics textbook which can be solved using algebra.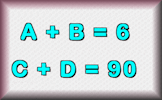 Superfluous Find a strategy to figure out the values of the letters used in these calculations.
Superfluous Find a strategy to figure out the values of the letters used in these calculations.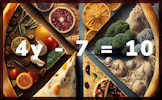 Solve To Find Fractions Find the value of the unknown in each of these linear equations. All of the answers are fractions
Solve To Find Fractions Find the value of the unknown in each of these linear equations. All of the answers are fractions Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise.
Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise. New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations.
New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations. Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.
Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.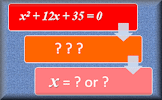 Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.
Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.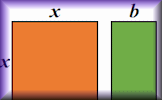 Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
Completing the Square Practise this technique for solving quadratic equations and analysing graphs. Inequalities Check that you know what inequality signs mean and how they are used to compare two quantities. Includes negative numbers, decimals, fractions and metric measures.
Inequalities Check that you know what inequality signs mean and how they are used to compare two quantities. Includes negative numbers, decimals, fractions and metric measures. Linear Programming A selection of linear programming questions with an interactive graph plotting tool.
Linear Programming A selection of linear programming questions with an interactive graph plotting tool. Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level.
Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level. Equations with Fractions Video If you have learnt how to solve linear equations the next step is to solve equations with fractions.
Equations with Fractions Video If you have learnt how to solve linear equations the next step is to solve equations with fractions. Algebraic Fractions A mixture of algebraic fraction calculations and simplifications.
Algebraic Fractions A mixture of algebraic fraction calculations and simplifications.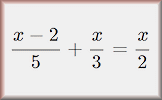 Equations with Fractions Practise solving linear equations that contain fractions in this multi-level exercise.
Equations with Fractions Practise solving linear equations that contain fractions in this multi-level exercise. Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Here are some exam-style questions on this topic:
- "Solve the following linear equations showing clearly each step of your working." ... more
- "The diagram shows an isosceles triangle (not drawn to scale)." ... more
- "The perimeter of the triangle is the same length as the perimeter of the square." ... more
- "The red line in the diagram below shows an inequality. If the variable is \(x\), which inequality best describes \(x\)?" ... more
- "(a) Solve 9m < 15m − 12" ... more
- "The graph of a quadratic function, \(y=f(x)\) is shown drawn accurately in the following diagram. Write down all the integer solutions of \(f(x) \le 0\)." ... more
- "Aimee, Natasha and Ruby play hockey." ... more
- "Julie is on holiday and buys \(x\) mangos, \((x+4)\) guavas and \((3x-5)\) bananas." ... more
- "The diagram below is a sketch of \(y = f(x)\) where \(f(x)\) is a quadratic function." ... more
- "Describe the unshaded (white) region by writing down three inequalities." ... more
- "Solve the following linear equation to find the value of \(x\)." ... more
- "On the grid below indicate the region that satisfies all three of these inequalities." ... more
- "The trapezium and rectangle shown here have the same perimeters. The diagrams are not drawn to scale and the measurements are in centimetres. Calculate the area of the trapezium." ... more
- "(a) The expression \( (x+1)(2x-3)(3x+4) \) can be written in the form \(ax^3 + bx^2 + cx + d \) where \(a, b, c\) and \(d\) are integers. Find the values of \(a, b, c\) and \(d\)." ... more
- "Two rectangles, not drawn to scale, are shown below. All measurements are in centimetres. Both rectangles have the same areas. Work out the perimeter of the rectangle on the left." ... more
- "A region on a coordinate grid is described by the following three inequalities:" ... more
- "By shading the unwanted regions, show the region satisfied by these three inequalities." ... more
- "Solve the following inequalities then explain how the whole number solutions to A and B different." ... more
- "The diagram shows part of the graph \(y=x^2-3x+6\)." ... more
- "A large car park has an area of 1400m2 with space for \(x\) cars and \(y\) vans. Each car requires 14m2 of space and each van requires 35m2 of space." ... more
- "(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\)." ... more
- "A region on a coordinate grid is described by the following three inequalities:" ... more
- "Show that you understand equations and inequalities by answering the following:" ... more
- "Here is a function machine that produces two outputs, A and B." ... more
- "In the diagram below, which is not drawn to scale, all dimensions are in centimetres and all angles are multiples of 90o. If the shaded area is 698cm2, work out the value of \(x\)." ... more
- "Given that:" ... more
- "Given that \(x^2 – 8x + 3 = (x – a)^2 – b\) for all values of x," ... more
- "Solve \(2x^2 + 7x - 15 <0\)" ... more
- "The area of triangle ABC (not drawn to scale) is " ... more
- "If \(y = 5x^4 + 3x^2\) and \(x=\sqrt{w+2}\), find \(w\) when \(y = 12\) showing each step of your working." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson

PYA
You have four minutes to write down as many equations as you can involving the given letters.
2nd Lesson

Connecting Rules
Give 20 rules connecting x and y given their values.
3rd Lesson

Lost Sheep
Which algebraic expression is the odd one out?
4th Lesson

Less Than
This mathematics lesson starter invites pupils to interpret a three part algebraic inequality.
5th Lesson

Mystic Maths
Work out why subtracting a two digit number from its reverse gives a multiple of nine.
6th Lesson

Same Same
A problem involving two people's ages which can be solved using algebra.
7th Lesson

Sum of the Signs
Each traffic sign stands for a number. Some of the sums of rows and columns are shown. What numbers might the signs stand for?
8th Lesson

Think Back
A problem which can be answered by forming an algebraic equation then solving it.
9th Lesson

Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.

