Transformations of Graphs
Term 2 starting in week 3 :: Estimated time: 2 weeks
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
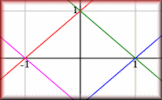 Graph Patterns Find the equations which will produce the given patterns of graphs.
Graph Patterns Find the equations which will produce the given patterns of graphs.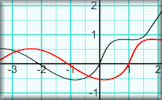 Transformations of Functions A visual aid showing how various transformations affect the graph of a function.
Transformations of Functions A visual aid showing how various transformations affect the graph of a function.
Here are some exam-style questions on this topic:
- "The graph of the curve A with equation \(y=f(x)\) is transformed to give the graph of the curve B with equation \(y=5-f(x)\)." ... more
- "(a) By completing the square, solve \(x^2+8x+13=0\) giving your answer to three significant figures." ... more
- "The graph of the following equation is drawn and then reflected in the x-axis" ... more
- "(a) Find the interval for which \(x^2 - 9x + 18 \le 0\)" ... more
- "(a) Write \(2x^2+8x+27\) in the form \(a(x+b)^2+c\) where \(a\), \(b\), and \(c\) are integers, by 'completing the square'" ... more
- "Let \(f (x)=a(x-b)^2+c\). The vertex of the graph of \(f\) is at (4, -3) and the graph passes through (3, 2)." ... more
- "A function is defined as \(f(x) = 2{(x - 3)^2} - 5\) ." ... more
- "\(f\) and \(g\) are two functions such that \(g(x)=3f(x+2)+7\)." ... more
- "Let \(f(x)=5x^2-20x+k\). The equation \(f(x)=0\) has two equal roots." ... more
- "Let \(f(x) = {x^2}\) and \(g(x) = 3{(x+2)^2}\) ." ... more
- "Part of the graph of a function, \(f\) , is shown in the following diagram. The graph of \(y = f(x)\) has a y-intercept at \((0, 1.5)\) , an x-intercept at \((a , 0)\) and horizontal asymptotes \(y = 5\) and \(y = -2\)." ... more
- "Let \(f\) and \(g\) be functions such that \(g(x) = 3f(x - 2) + 7\) ." ... more
- "The graph of \( y = f(|x|) \) for \( -2 \leq x \leq 2 \) is shown in the following diagram." ... more
- "Two functions are defined as follows: \(f(x) = 2\ln x\) and \(g(x) = \ln \frac{x^2}{3}\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.

