Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Just in case you were wondering, this is the Transum Mathematics newsletter for the month of September 2020 and as Talk Like A Pirate Day will occur during this month I thought I’d give an old Russian puzzle a pirate theme:
Two shipmates, Scally and Wag, had been up to mischief hacking the ship’s pirateware. Captain Scurvy decided to give them a chance of freedom before making them walk the plank. Scally was put into a small boat tethered to the port side of the ship and Wag was in a boat to the starboard side. Over the deck of the ship lay six ropes each with one end dangling above Scally’s boat and the other end dangling above Wag’s.
Scurvy ordered the shipmates to tie the ends of the ropes together in pairs. Neither could see what the other was doing so did not know how the other had paired up the ropes. If, after the tying, the six ropes formed one large loop the shipmates would walk free. What is the probability of this happening?
The answer is at the end of this newsletter but if you peep too soon you will walk the plank!
September is traditionally Back To School month in the UK but since I started working in International schools in 1997 I learned very quickly how to write an August date on the board as the whole academic year begins a few weeks earlier as it does in Scotland. Those of you in the southern hemisphere will have been back at school for what must seem like a very long time by now. Nevertheless my best wishes to anyone about to start a new school year and I hope you find the Back To School resources useful.
Transformation Tetris, the classic computer game with a mathematical connection, was added to the website last month. I’ve managed translations and rotations but reflections are still on the ‘to do’ list. It’s still lots of fun regardless.
A new resource called Get A Wiggle On has been created as the Starter of the Day for 2nd March. I had at last succumbed to making my version of the mental arithmetic challenge that appears in some newspapers. My version however is dynamic and there is the choice to let pupils work through the rows in their own time or to keep up with the blocks appearing on screen. As a subscriber you have access to controls lower down the page to vary the speed and number of rows that will appear.
Another new resource called Sum=Product has been created as the Starter of the Day for 12th August. Keep scrolling down the panels until you find the level of difficulty that will best suit your pupils. Lots of arithmetic will be required to come up with the answers. More able learners will possibly find all of the solutions and be able to explain why there are no more.
A colourful video has been made to help pupils do the Venn Paint exercise and just last week I uploaded a video called Perpendicular Bisector which leads into the fascinating world of Voronoi Diagrams. The newest video however is all about Bearings and can be found in the help tab of that exercise.
I have a cupboard in my office that contains my collection of Toblerone, Pringle and chocolate boxes which I use occasionally to illustrate 3D shapes. Last week I added this to my collection. A rare heptagonal prism (roughly). Do you know what it is designed to be used for?
Now the answer to the puzzle of the month. The diagram below shows the six ropes after Scally had done his knot tying. If Wag ties end A to end B then they are doomed to walk the plank as this would prevent a large loop of all six ropes being formed. There is a four fifths chance of this not happening.
Let’s consider that Wag ties end A to end C. Now end B must be tied to either end E or end F for the mission to be a success. There is a two thirds chance of this happening so the overall probability is:
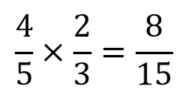
As this probability is greater than a half they are more likely to walk free than walk the plank.
That's all for now. Take care of yourself and, if you can, someone else too.
PS. How many times can you subtract 7 from 83, and what is left afterwards?
Answer: I can subtract it as many times as I want, and it leaves 76 every time!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
