International Baccalaureate Mathematics

Syllabus Content

Indefinite integral of xⁿ,sinx,cosx,1/x and e^x. The composites of any of these with the linear function ax+b. Integration by inspection (reverse chain rule) or by substitution for expressions of the form: ∫kg'(x)f(g(x))dx

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

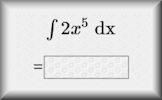Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions.

Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.

Here are some exam-style questions on this statement:

"The graph of $f(x)=8-x^2$ crosses the x-axis at the points A and B." ... more

"The acceleration, $a$ ms^-2 , of an object at time $t$ seconds is given by" ... more

"(a) Find $\int (4x+5) dx$." ... more

"Given that $ \frac{dy}{dx} = \sin(x + \frac{\pi}{3})$ and $y = 5$ when $x = \frac{8\pi}{3}$, find $y$ in terms of $x$." ... more

"(a) Find $ \frac{dy}{dx} $ when:" ... more

"Consider the graph of the function $f(x)=x^2+2$." ... more

"(a) Express the algebraic fraction" ... more

"Make a sketch of a graph showing the velocity (in $ms^{-1}$) against time of a particle travelling for six seconds according to the equation:" ... more

"Find the value of $a$ if $\pi \lt a \lt 2\pi$ and:" ... more

"This graph represents the function $f:x\to a \cos x, a\in \mathbf N$" ... more

"Find $f(x)$ if $f'(x)=6 \sin2x$ and the graph of $f(x)$ passes through the point $(\frac{\pi}{3},11)$." ... more

"Consider the function $f$ defined by $f(x) = 25e^{x-5}$ for $x \in \mathbb{R}^+$." ... more

"The following diagram shows the graph of $f(x) = \cos(e^x) \; \text{for} \; 0 \le x \le 0.5$." ... more

"Find $f(x)$ if:" ... more

"Let $f(x) = \frac{ln3x}{kx} $ where $ x \gt 0$ and $ k \in \mathbf Q^+ $." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Calculus It is said that the word calculus comes from the Latin word for the small pebble used for counting and calculations. The two major branches, differentiation and integration, are studied by pupils only towards the end of their school days but does then form a major part of their studies. A course in calculus is a prerequisite for other, more advanced courses in mathematical analysis.

Furthermore

Official Guidance, clarification and syllabus links:

$ \int \frac{1}{x} \; dx = \ln{|x|} + C$

Example of composites:

$ f'(x)=\cos(2x+3) \; \Rightarrow \; f(x)= \frac12 \sin(2x+3) + C $

Examples of inspection and substitution:

$ \int 2x(x^2 + 1)^4 \; dx, \quad \int 4x\sin{x^2} \; dx, \quad \int \frac{\sin x}{\cos x} \; dx $

Formula Booklet:

Standard integrals

$ \int \frac{1}{x} \; dx = \ln{|x|} + C$

$ \int \sin x \; dx = - \cos x + C$

$ \int \cos x \; dx = \sin x + C$

$ \int e^x \; dx = e^x + C$

Integration by inspection, also known as the reverse chain rule, is a technique used to simplify the process of integration for certain functions. When faced with an integrand of the form $ \int k g'(x)f(g(x)) \; dx $, one can recognise that the derivative of some function is present, allowing for a more straightforward integration.

To apply this method, we look for a function whose derivative matches a part of the integrand. If $ u = g(x) $, then $ du = g'(x) \; dx $. By substituting these values into the integral, the expression often simplifies, making it easier to evaluate.

Example:

Consider the integral:

$$ \int x \sin(x^2) \; dx $$

Here, we can let $ u = x^2 $. This gives $ \frac{du}{dx} = 2x $ or $ du = 2x \; dx $. Making the substitution, we get:

$$ \int \frac{1}{2} \sin(u) \; du $$

This integral is now straightforward to evaluate:

$$ -\frac{1}{2} \cos(u) + C $$

Re-substituting for $ u $, we obtain the final result:

$$ -\frac{1}{2} \cos(x^2) + C $$

This video on Integration Rules is from Revision Village and is aimed at students taking the IB Maths AA SL/HL course.

This video on Integration by Substitution is from Revision Village and is aimed at students taking the IB Maths AA SL/HL course

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.