Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Pin Drop Estimate the probability of a drawing pin landing point up from experimental data.
Pin Drop Estimate the probability of a drawing pin landing point up from experimental data. Probability Video A reminder of how to work out basic probability leading to simple combined events and expected values.
Probability Video A reminder of how to work out basic probability leading to simple combined events and expected values. Probability Basic probability questions in an online exercise.
Probability Basic probability questions in an online exercise. Snail Race Projectable Twelve snails have a race based on the sum of two dice. This is the teachers' version of the race simulation.
Snail Race Projectable Twelve snails have a race based on the sum of two dice. This is the teachers' version of the race simulation. Two Dice Possibility Space An interactive visual aid showing the possibility space obtained when throwing two dice
Two Dice Possibility Space An interactive visual aid showing the possibility space obtained when throwing two dice Snail Race A race between 12 snails. Which snail is most likely to win? This is the students' version of the race simulation.
Snail Race A race between 12 snails. Which snail is most likely to win? This is the students' version of the race simulation. The Maths of Gambling Gambling is never a good idea and this activity might help you understand the mathematics involved.
The Maths of Gambling Gambling is never a good idea and this activity might help you understand the mathematics involved.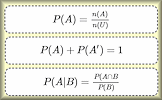 Probability Formulae Show that you know which formula (as given in the IB Formula Booklet) to use for each probability question. A drag and drop challenge.
Probability Formulae Show that you know which formula (as given in the IB Formula Booklet) to use for each probability question. A drag and drop challenge.
Here are some exam-style questions on this statement:
- "The following table shows the probabilities of winning certain prizes at a stall in Faulton Towers theme park. A prize is always given for every turn." ... more
- "Derren thinks he is a mind reader and can tell what Paige is thinking. An experiment was conducted to test this." ... more
- "At the Trantown annual Fayre there are a number of different sideshows designed to raise money for cancer research. Roger is looking after two of these, the lucky dip and the raffle." ... more
- "The table shows the shoe sizes of 35 male teachers." ... more
- "Aran, Betsy and Connor collect data about which way up a drawing pin will land if dropped from a fixed height. Here are their results." ... more
- "During a demonstration for Year 10 pupils a biased coin in a computer simulation landed on heads 600 times." ... more
- "Donna is in a class of 25 students, 5 of whom have a pet dog." ... more
- "On a Tuesday at a theme park, a sample of 50 visitors was randomly selected as they were leaving the park. They were asked how many times that day they had been on a ride called The Serpent. This information is summarised in the following frequency table." ... more
- "Piers wins one of the many prizes on offer in the school raffle but he does not yet know exactly what the prize is.
- The probability that a prize is something to eat is 0.3
- The probability that a prize is worth more than $10 is 0.2
- The probability that a prize is something to eat or worth more than $10 is 0.4
Find the probability that the prize Piers wins is not both something to eat and worth more than $10 as Piers does not like expensive food.
" ... more - "A game at a fayre consists of a players throwing one dart at the board pictured below.
The probability of hitting each region and the points scored for hitting that region is given in this table.
" ... more
Here are some Advanced Starters on this statement:
- Biased Coin
Use a biased coin to obtain a fair result more - How Many Left Handers?
Work out the number of members if the probability of left-handed members being randomly selected is given. more - One Candle Each
What are the chances of getting a candle on each piece of birthday cake? more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
In probability theory, a trial refers to a single occurrence or performance of a random experiment. The result of a trial is called an outcome. When each outcome in a sample space is equally probable, they are termed as equally likely outcomes. The relative frequency of an event is the ratio of the number of times the event occurs to the total number of trials. The set of all possible outcomes of an experiment is termed the sample space, denoted by \( U \). An event is a subset of the sample space, representing a specific set of outcomes. The probability of an event \( A \) is given by \( P(A) = \frac{n(A)}{n(U)} \), where \( n(A) \) is the number of outcomes in event \( A \) and \( n(U) \) is the total number of outcomes in the sample space. Complementary events refer to events that are mutually exclusive to each other. If \( A \) is an event, then \( A' \) (or not \( A \)) is the event that \( A \) does not occur. The expected number of occurrences of an event is the number of times we expect the event to occur in a given number of trials, based on its probability.
Key Formulae:
$$ P(A) = \frac{n(A)}{n(U)} $$
$$ P(A') = 1 - P(A) $$
$$ \text{Expected number of occurrences} = \text{probability of event} \times \text{number of trials} $$
Example:
Consider a fair six-sided die. The sample space \( U \) is \( \{1, 2, 3, 4, 5, 6\} \). Let event \( A \) be the event that the die shows an even number. So, \( A = \{2, 4, 6\} \).
Using the formula, the probability of event \( A \) is:
$$ P(A) = \frac{n(A)}{n(U)} = \frac{3}{6} = \frac{1}{2} $$
Thus, if we roll the die 100 times, the expected number of times we get an even number is:
$$ \text{Expected number of occurrences} = \frac{1}{2} \times 100 = 50 $$
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

