Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
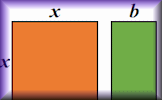Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
Circle Theorems Diagrams of the circle theorems to be projected onto a white board as an effective visual aid.
Circle Theorems Exercise Show that you understand and can apply the circle theorems with this self marking exercise.
Circle Theorem Pairs A pairs game based around ten theorems about the angles made with chords, radii and tangents of circles.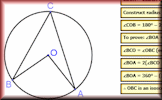
Proof of Circle Theorems Arrange the stages of the proofs for the standard circle theorems in the correct order.
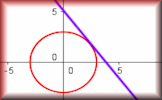Circle Equations Recognise and use the equation of a circle with centre at the origin and the equation of a tangent to a circle.
Here are some exam-style questions on this statement:
- "B, C, D and E are points on the circumference of a circle, centre O." ... more
- "What is the equation of a circle, centered at the origin, that has a tangent passing through the points (-30, 0) and (0, -15)?" ... more
- "The diagram shows a circle with equation \(x^2+y^2=13\)." ... more
- "(a) Find the coordinates of the point at which the curve \(y = k^x\) intersects the y-axis." ... more
- "A circle with equation \(x^2 + y^2 = 6 \) meets a one of its tangents at point \(S\)." ... more
- " (a) The circumference of a circle is \(16 \pi \) cm and its centre is at the origin. Find the equation of the circle." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Circles This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation. Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations. More mathematics related to the circle can involve angle theorems, loci and algebra.
- Coordinates It is important that pupils become proficient at understanding coordinates at a basic level before using them in their study of graphs. Plotting points and finding the coordinates of points are the pre-requisite skills for studying a number of branches of mathematics. The Cartesian plane consists of a horizontal x-axis and a vertical y-axis that intersect at the origin (0, 0). The mathematician René Descartes developed the concept of the Cartesian plane while lying in bed one morning and observing a fly on the ceiling! Pupils should learn the conventions starting with knowing that the horizontal axis is the x-axis and the vertical axis is the y-axis (remember x is a cross so the x axis is across!). The axes meet at the origin which has coordinates (0,0). Coordinates are written as two numbers separated by a comma and contained inside brackets. For example (3,9) means the point is above 3 on the x-axis and level with 9 on the y-axis. To get to this point from origin you go along 3 and up 9 (remember to go along the hall before going up the stairs or that pole vaulter has to run along before leaping up into the air!). Coordinates can be positive or negative (remember points to the right of the origin have a positive x-coordinate – being positive is right!). The abscissa often refers to the horizontal coordinate of a point and the ordinate refers to the vertical coordinate. In three dimensions, three perpendicular lines are defined as the axes and the coordinates of each point is defined with three numbers.
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
Furthermore
This video on Completing The Square is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
