Angles and bearings
Term 2 starting in week 1 :: Estimated time: 2 weeks
- Use cardinal directions and related angles (review)
- Draw and interpret scale diagrams (review)
- Understand and represent bearings
- Measure and read bearings
- Make scale drawings using bearings
- Calculate bearings using angles rules
- Solve bearings problems using Pythagoras and trigonometry
For higher-attaining pupils:
- Solve bearings problems using the sine and cosine rules
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Scale Drawings Measure line segments and angles in geometric figures, including interpreting scale drawings.
Navigation NEWS Each visitor to this page has a unique maze constructed for them to find their way through answering questions about bearings along the way.
Plane Bearings A visual aid designed to help pupils estimate three figure bearings.
Map Scales Video Refresh your understanding of map scales expressed as ratios.
Map Scales Test your understanding of map scales expressed as ratios with this self marking quiz.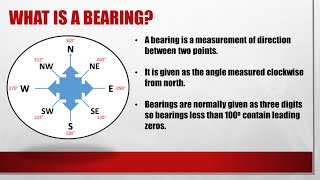
Bearings Video Find out about bearings and practise estimating, measuring and calculating them.
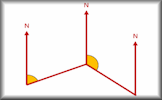Bearings Practise your ability to interpret and use three-figure bearings with this self-marking exercise.
Scale Factors Video The scale factor, area factor and volume factor of similar shapes are quite different.
Similar Shapes Questions about the scale factors of lengths, areas and volumes of similar shapes.
Here are some exam-style questions on this topic:
- "The diagram show the locations of three orienteering checkpoints. What is the three-figure bearing of A from B?" ... more
- "The diagram shows the positions of three towns, Aberville (A), Buchus (B) and Clipton(C)." ... more
- "A fishing boat is somewhere along the line from A to C." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Bearings A bearing is a description of a direction. It is the number of degrees measured in a clockwise direction from north as seen from above. Convention, probably born out of the need to be quite clear when saying a bearing over a crackly aircraft radio or storm at sea, three figures are given for each bearing. So 90 degrees would be expressed as 090 degrees. The four main directions are known as the cardinal points. These are north (360°), east (090°), south (180°) and west (270°). The directions in between those are known as the half cardinal points and can be expressed as north-east (045°), south-east (135°), south-west (225°) and north west (315°). The study of bearings in Mathematics provides a practical, real-life application of angles and geometry. It can provide a need for numerical calculations, scale drawing and estimation.
- Ratio A ratio is a relationship between two numbers of the same kind. In layman's terms a ratio represents, simply, for every amount of one thing, how much there is of another thing. This topic presents a number if different ways pupils can represent ratios and apply their meaning to problem solving situations.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
News Common
Follow the compass directions given in the squares to find where the route starts?
2nd Lesson
Air Traffic Control
Work out which aircraft are in danger of colliding from their positions and direction of travel. An exercise in understanding bearings.
3rd Lesson
No Partner
Find which numbers in a given list do not combine with other numbers on the list to make a given sum.
4th Lesson
Pipeline Puzzle
Arrange the numbers so that the totals of the three numbers along any pipe are the same.
5th Lesson
Polygon Riddle 2
A "My first is in..." type riddle leading to a polygon interior angle calculation.
6th Lesson
Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
