More Functions
Term 1 starting in week 10 :: Estimated time: 3 weeks
- 2.8 Rational functions.
- 2.9 Exponential and logarithmic functions.
- 2.10 Solving equations.
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
 What is e? Dr James Grime discusses e - the famed Euler's Number.
What is e? Dr James Grime discusses e - the famed Euler's Number. Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations.
Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations. Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication.
Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication. Using A Calculator Questions to test your ability to use a basic calculator, scientific calculator and a graphic display calculator.
Using A Calculator Questions to test your ability to use a basic calculator, scientific calculator and a graphic display calculator. Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function.
Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function. Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds. Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.
Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.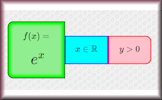 Domain, Range and Asymptotes Match the functions with their features. A drag and drop activity.
Domain, Range and Asymptotes Match the functions with their features. A drag and drop activity. Logarithms Self-marking exercises on evaluating logarithms and using them to solve equations.
Logarithms Self-marking exercises on evaluating logarithms and using them to solve equations.
Here are some exam-style questions on this topic:
- "Sketch the graph of \(y=0.5^x +1\) for \(0 \le x \le 5\) labeling the y intercept." ... more
- "While studying a new disease, scientists found that the number of toxic cells in the bloodstream increased over time, according to the model \(D(t)=12×(1.16)^t , t \ge 0\) where \(D\) is the number of the toxic cells in the bloodstream per litre and \(t\) is the time in hours." ... more
- "(a) Sketch the graph of \( y = f(x) \) for values of \( x \) between \(-5\) and \(5\) given that:" ... more
- "Percy Cod and Fran Finklestein are both researchers working at different universities. They are each studying a different colony of bacteria which coincidentally start increasing in size at the same time." ... more
- "The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre." ... more
- "The quantity of heat required to heat an amount of water is given by the formula:" ... more
- "Consider the following function for \(-2 \le x \le 2\)." ... more
- "The function \( f \) is defined by \( f(x) = \frac{5x + 5}{3x - 6} \) for \( x \in \mathbb{R}, x \neq 2 \)." ... more
- "A function \(f\) is defined by \(f(x) = 2 + \dfrac{1}{3-x}, \text{ where } x \in \mathbb{R}, x \neq 3.\)" ... more
- "Find the value of the following:" ... more
- "Evaluate the following, giving your answers as integers." ... more
- "Find the value of" ... more
- "Find the range of possible values of \(a\) such that \(5e^x - \ln{a} = e^{2x}\) has at least one real solution." ... more
- "The Big Wheel at Fantasy Fun Fayre rotates clockwise at a constant speed completing 15 rotations every hour. The wheel has a diameter of 90 metres and the bottom of the wheel is 6 metres above the ground." ... more
- "The Fun Wheel at the Meller Theme Park rotates at a constant speed." ... more
- "(a) Solve \(4x^2 - 8x - 5 = 0\)" ... more
- "In medical imaging, the radioactive isotope Technetium-99m is used due to its short half-life of 6 hours. After being introduced into the body, the isotope decays, and the amount of Technetium-99m present can be tracked over time to study the function of specific organs." ... more
- "A cup of hot tea is placed on a table to cool. The temperature of the room is 24oC." ... more
- "Let \(f(x)=\frac{3x}{x-q}\), where \(x \neq q\)." ... more
- "The widest river in the world has a width of 11km at its widest point. Suppose there were a straight length of this river near Awkwardville (A) as shown in the diagram below. Points A and P lie on opposite banks, such that AP is the shortest distance across the river. Point B represents the centre of Bumblingburg which is located on the southern riverbank." ... more
- "In a remote lake it was noticed by conservationists that a disease was rapidly spreading amongst two species of fish, R and S, which is reducing their numbers. The conservationists calculated that the numbers of each type of fish can be modelled by the functions:" ... more
- "Consider the function \(f (x) = \log_p(24x - 18x^2)\) , for \(0 \lt x \lt 1\), where \(p \gt 0\)." ... more
- "Let \(f(x) = \frac{9x-3}{bx+9}\) for \(x \neq -\frac9b, b \neq 0\)." ... more
- "Fifty milligrams of a certain type of medicine has been shown to enter the bloodstream of an adult according to the following equations:" ... more
- "The height above the ground, H metres, of a passenger on a Ferris wheel t minutes after the wheel starts turning, is modelled by the following equation:" ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
- Logarithms Older teachers will remember their school days, before calculators were widely available, using logarithms to perform difficult multiplication and division calculations. Nowadays logarithms, or logs as they are more commonly known, are studied as part of an A Level and International Baccalaureate course and are seen as being useful for solving certain exponential equations. Basically a logarithm is the inverse function to exponentiation.

