Mathematics Topics.
Algebra
Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas.
If this topic were split into four sub topics they might be:
Creating and simplifying ex
Expanding and factorising ex
Substituting and using formulae;
Solving equations and real life problems;
This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
Angles
Pupils should understand that angles represent an amount of turning and be able to estimate the size of angle. When constructing models and drawing pupils should be able to measure and draw angles to the nearest degree and use appropriate language associated with angles.
Pupils should know the angle sums of polygons and that of angles at a point and on a straight line. They will learn about angles made in circles by chords, radii and tangents and recognise the relationships between them.
Pupils will work with angles using trigonometry, transformations and bearings. In exams pupils are often instructed that while non-exact answers should be given to three significant figures, angle answers should be given to one decimal place.
Approximation
Approximating a quantity is often to get a value that is easier to use or understand, at the cost of making it less precise. This approximation is very important in dealing with answers to mathematical problems and making them relevant to the real world. Rounding to a given number of decimal places or significant figures is required of pupils.
The error introduced when approximating a value may be further magnified with subsequent calculations. Understanding this error and how it can be minimised is another important aspect of this topic.
See also the "Rounding" and "Estimating" Topic pages.
Area
Pupils should not only be able to remember and apply area formulae but they should also have a good understanding of what area means. This can be achieved by beginning the study of area with plenty of practical examples. The Pin Board provides an open-ended interactive experimental environment to secure a good fundamental understanding of area.
Some examinations provide formulae sheets but it is still important that pupils know the common formulas for finding the areas of basic shapes. They should use these formulae in context to find areas of basic and compound shapes and be able to give answers using appropriate units.
Pupils will also learn to find the surface areas of three dimensional shapes, use scale to determine areas from maps and solve real world problems involving areas.
See also the topics called Measures, Shape (3D) and Ratio.
Arithmetic
The ability to perform mathematical calculations is still very important despite our hi-tech environment. Good numeracy skills support the understanding of more advanced mathematical concepts at all levels. Mathematicians still consider mastery of the manual algorithms to be a necessary foundation for the study of algebra and computer science.
Pupils should have a good grasp of the meaning of numbers and use their understanding of place value to multiply and divide whole numbers and fractions. They should be able to order, add and subtract negative numbers in context. They should use all four operations
with decimals rounding answers where required. They should be able to solve simple problems involving ratio and direct proportion and calculate fractional or percentage parts of quantities and measurements, using a calculator where appropriate.
See also the Mental Methods topic and our Number Skills Inventory.
Averages
"Average" is a very general term that is used commonly in everyday English and most people have an idea what it means. Mathematicians like to be a little more precise however and have come up with a number of different ways of finding a measure of central tendency.
Pupils at school should develop their understanding of averages so that they can more precisely communicate information to others and are not misled by statistics presented in a way to distort the facts.
Pupils should understand and use the mean of discrete data. They should be able to compare two simple distributions using the range and one of the mode, median or mean.
See also the topics called Data Handling and Statistics.
Bearings
A bearing is a description of a direction. It is the number of degrees measured in a clockwise direction from north as seen from above. Convention, probably born out of the need to be quite clear when saying a bearing over a crackly aircraft radio or storm at sea, three figures are given for each bearing. So 90 degrees would be expressed as 090 degrees.
The four main directions are known as the cardinal points. These are north (360°), east (090°), south (180°) and west (270°). The directions in between those are known as the half cardinal points and can be expressed as north-east (045°), south-east (135°), south-west (225°) and north west (315°).
The study of bearings in Mathematics provides a practical, real-life application of angles and geometry. It can provide a need for numerical calculations, scale drawing and estimation.
Calculator
All pupils should learn to calculate accurately, selecting mental methods or calculating devices as appropriate. Pupils, through practice, should learn to use the most appropriate method to perform a calculation. It is appropriate for them to use a calculator when performing a calculation without a calculator will take an inappropriate amount of time.
In addition to simply finding answers, calculators provide a fascinating opportunity for pupils to investigate number patterns, properties and relationships. They can easily use a calculator to learn more about Mathematics through open ended explorations, games and puzzles.
On this website you can find activities which help pupils practise calculator skills and become more familiar with this essential tool whether it be basic, scientific or a graphic display calculator (GDC).
To specifically practise using a GDC there is nothing better than our Exam-Style Questions which include worked solutions, many of which contain screen shots of the TI-nSpire GDC.
Calculus
It is said that the word calculus comes from the Latin word for the small pebble used for counting and calculations. The two major branches, differentiation and integration, are studied by pupils only towards the end of their school days but does then form a major part of their studies. A course in calculus is a prerequisite for other, more advanced courses in mathematical analysis.
Isaac Newton is best known for developing calculus. He was born in England in 1642 and is considered one of the most influential scientists and mathematicians in history.
Circles
This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation.
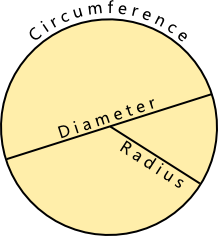
Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations.
More mathematics related to the circle can involve angle theorems, loci and algebra.
Combinations
"A combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange." - Wikipedia
In Primary school pupils should practise sorting and grouping items noting similarities and differences. They should develop strategies for finding all the ways a small number of items can be arranged so that missing or duplicates can be found quickly.
By the end of Secondary school pupils will have learnt the formulas for combinations and permutations and apply them when solving probability problems.
Construction
In a way this topic is quite different to all of the other topics in school mathematics. It requires a practical skill as well as the understanding of the geometrical concepts. It also requires a sharp pencil, a sturdy ruler and a decent pair of compasses.
Younger children should practise using the drawing instruments to make patterns. They will then progress to constructing accurate diagrams, plans and maps.
Older pupils are taught to derive and use the standard ruler and compass constructions for the perpendicular bisector of a line segment, the perpendicular to a given line from a given point and the bisector of a given angle.
Coordinates
It is important that pupils become proficient at understanding coordinates at a basic level before using them in their study of graphs. Plotting points and finding the coordinates of points are the pre-requisite skills for studying a number of branches of mathematics.
The Cartesian plane consists of a horizontal x-axis and a vertical y-axis that intersect at the origin (0, 0). The mathematician René Descartes developed the concept of the Cartesian plane while lying in bed one morning and observing a fly on the ceiling!
Pupils should learn the conventions starting with knowing that the horizontal axis is the x-axis and the vertical axis is the y-axis (remember x is a cross so the x axis is across!). The axes meet at the origin which has coordinates (0,0).
Coordinates are written as two numbers separated by a comma and contained inside brackets. For example (3,9) means the point is above 3 on the x-axis and level with 9 on the y-axis. To get to this point from origin you go along 3 and up 9 (remember to go along the hall before going up the stairs or that pole vaulter has to run along before leaping up into the air!).
Coordinates can be positive or negative (remember points to the right of the origin have a positive x-coordinate – being positive is right!).
The abscissa often refers to the horizontal coordinate of a point and the ordinate refers to the vertical coordinate.
In three dimensions, three perpendicular lines are defined as the axes and the coordinates of each point is defined with three numbers.
Creativity
We often hear the term creativity used in terms of art, music or drama. This higher order thinking skill has a big part to play in Mathematics. We endeavour to develop creative problem solving strategies and investigative techniques in our pupils by providing them with motivating open ended situations to think about.
Data Handling
Data is talked about more this decade than ever before. Whether it be how social media companies deal with your personal data or how analysing data can improve algorithms for systems that make everyday life easier or more profitable.
Pupils are first introduced to small, familiar data sets and learn to visualise them in many different ways. They may produce their own data from experiments, observations or games and will then describe their data in different ways.
Pupils will calculate averages and other summary measures (mean, median, mode range) and produce bar charts, pie charts and box plots.
Older pupils will use technology to help analyse larger data sets and will be introduced to inter-quartile range and standard deviation. They will draw conclusions from scatter diagrams, and have a basic understanding of correlation. They will learn how to apply statistical information to calculate probabilities.
See also the topics called Statistics, Averages and Probability.
Decimals
Working with decimals, for most pupils, presents little difficulty if the pupils have confidence working with whole numbers. The topic of decimals provides an extension to the place value system with the addition of tenths, hundredths, thousandths etc.
For many pen and paper multiplication and division calculations the decimal numbers can be considered as whole numbers then the answers adjusted accordingly. So 2.4 x 2.34 can be considered as 24 x 234 ÷ 1000. The numbers are multiplied by ten and one hundred respectively then the answer needs to be divided by the ten and one hundred to compensate.
Pupils should use their understanding of place value to round decimal numbers. They should also use decimal numbers in the context of measures and money. This topic also contains activities which encourage pupils to investigate and explore the properties of decimal numbers and gain a better understanding of them.
Enlargements
When areas and volumes are enlarged the results are far from intuitive. Doubling the dimensions of a rectangle produces a similar shape with four times the area! Doubling the dimensions of a cuboid produces a similar shape with eight times the volume!
The activities provided are intended to give pupils experiences of dealing with enlargements so that they better understand the concept and are able to produce diagrams, make models and answer questions on this subject.
Once positive integer scale factors have been mastered the notion of fractional and negative scale factors await discovery!
Estimating
The ability to estimate values is an often overlooked part of Mathematics. Estimating lengths, weights, time, angles and solutions to problems should be practised regularly. Pupils should make sensible estimates of a range of measures in relation to everyday situations.
A basic ability to estimate quantities without counting, like when choosing a checkout line at the supermarket, can be called a person’s innate ‘number sense’. Practising this kind of estimating may actually improve a pupil’s ability in other areas of mathematics. This is one of the findings of research published in Psychological Science, a journal of the Association for Psychological Science.
Practising estimation can be a lot of fun when presented as a game, challenge or group activity and provides the opportunity for the teacher to introduce variety in the mathematics classroom.
Factors
A factor is a whole number that divides exactly into another whole number. We say the first number is a factor of the second number. Prime numbers only have two factors, one and themselves.
After becoming familiar with times tables pupils then practise using this knowledge by recognising factors of numbers. There are well known and some less well known divisibility tests that are of some use in solving more complex number problems.
Pupils need to know how to find the highest common factor (HCF) of two or more numbers either mentally or using a pen and paper strategy so that they can correctly manipulate fractions and algebraic expressions.
Fractions
A fraction is a part of a number. Fractions are either vulgar or decimal. Vulgar fractions can be proper, improper or mixed. Equivalent fractions have the same value.
Pupils, at all stages of their learning, should practise using fractions. From dealing with halves, the most basic fraction, to manipulating algebraic fractions containing surds, this topic is always relevant. Proficiency also depends on reasonable numeracy skills particularly the multiplication tables and finding the lowest common multiple of two numbers. Pupils also need to be able to convert vulgar fractions to decimals and percentages and vice versa.
Be wary of teaching the 'rules' for manipulation fractions by rote. Pupils need to understand the reason why and the time-honoured key to understanding starts with the imaginary pizza and the much-used fraction wall.
Fun
If you are looking for fun and games for the end of term the best place to start is the Fun Maths page where you'll find lots of enjoyable activities all with a mathematical theme.We also have Maths Games and a number of Strategy Games which, while not being explicitly mathematical, involve similar thought processes to solving mathematical problems. They are ideal for two people sharing one computer.
Functions
A relationship between two sets can be called a mapping. Elements of the first set (domain) are mapped to elements of the second set (range). A function is a special type of mapping for which one value in the domain maps to one, and only one value in the range.
Pupils in Primary school will use the concept of function machines to perform calculations. They will then learn to ‘work backwards’ to find the inverse function. The study of functions becomes more formal as pupils become more proficient and able to cope with more complex mathematical ideas.
Games
Make drill and practice fun by turning it into a game! Playing against a friend adds an extra incentive to do well. The memory game (Kim's game) can be used for general revision as it involves a number of different mathematical topics.
See also Fun Maths and the main Games page.
We also have a number of Strategy Games which, while not being explicitly mathematical, involve similar thought processes to solving mathematical problems. They are ideal for two people sharing one computer.
Geometry
Geometry is a branch of mathematics concerned with
questions of shape, size, relative position of figures, and the properties of
space. Geometry arose independently in a number of early cultures as a body of
practical knowledge concerning lengths, areas, and volumes, with elements of a
formal mathematical science emerging in the West as early 6th Century BC.
See also the topics of
Angles,
Area,
Bearings,
Circles,
Enlargements,
Mensuration,
Pythagoras,
Shape,
Shape (3D),
Symmetry,
Transformations and
Trigonometry.
Graphs
This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts.
A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values.
Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops.
Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
Indices
Where do many fish live? Indices (in the seas!) This topic involves the use of the index, power or exponent. The concept is easily misunderstood and a surprisingly large number of pupils will evaluate 62 as 12 and not 36.
After having mastered positive integer indices pupils should move on to negative indices and fractional indices. Exploring this topic in both numeric and algebraic ways will provide understanding and competence in this important concept.
Investigations
An investigation, as defined by a dictionary, is a searching enquiry for ascertaining facts. In mathematics this enquiry is a journey into the unknown without a map. Pupils should enjoy choosing the direction they will take in exploring a situation which has been described in an open-ended way. They will also develop pride in describing their findings to their classmates and may even stumble across findings that will suprise their teacher.
Take a look at our main page of investigation starting points which can be the seed of creative and exciting course work.
LCM
LCM stands for lowest common multiple or least common multiple. The LCM of two (or more numbers) is the smallest number that both of the numbers divide into exactly. Being able to find the LCM is useful when trying to find a common denominator when adding two fractions together. The LCM also describes the points when two (or more) periodic repetitions coincide.
HCF stands for highest common factor which is also known as the greatest common factor. The HCF of two (or more) numbers is the largest number that divides into the two numbers exactly. Being able to find the HCF is useful in everyday organisational tasks and also when factorising algebraic expressions.
Live Data
One of the big differences between Maths from a textbook and Maths from the web is the possibility of using live data. This possibility gives problem solving real context and allows investigating statistical connections to be far more meaningful.
Loci
A locus (plural: loci) is a set of points whose location satisfies or is determined by one or more specified conditions. This topic links to Geometry and Shape and provides opportunity for accurate drawing and 'people maths' where pupils can position themselves in the classroom according to certain conditions.
Logarithms
Older teachers will remember their school days, before calculators were widely available, using logarithms to perform difficult multiplication and division calculations. Nowadays logarithms, or logs as they are more commonly known, are studied as part of an A Level and International Baccalaureate course and are seen as being useful for solving certain exponential equations. Basically a logarithm is the inverse function to exponentiation.
The person who is most commonly credited with the invention of logarithms is the British mathematician John Napier
Logic
Wouldn't it be nice to live in a world where everything obeyed the rules and operated as predicted? This area of Mathematics explores the fundamentals of logical thinking and its application in problem solving.
This topic contains games, puzzles and activities that require the pupil to analyse a situation, understand the constraints, connections and rules in order to solve a problem, find a solution or win a challenge.
Learning how to operate in a very precise, logical way is the fundamental nature of being a good student of Mathematics.
Memory
If pupils have immediate, effortless recall of mathematical facts their brain's working memory is better able to solve more complex problems. A pupil can exercise their memory in order that it can improve and this topic provides activities to do just that.
Pupils need to memorise their multiplication tables and other number facts as well as geometrical theorems and algebraic techniques. They need to remember the correct names for shapes, operations and processes and they need to know how to apply this knowledge to solving problems.
The memory activities provided are generally great fun if presented in the right way and provide variety to the other activities of the typical mathematics lesson.
Mensuration
Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume. It is linked closely to the topic of Estimation and related to the topics of Angles, Shape and Shave (3D).
It is essential for pupils to have an understanding of the units used to measure which include both the more common metric units and the Imperial units still in common usage. We have found a good teaching strategy is to ask each of the pupils to "Bring to the next Maths lesson some visual aid which will help the rest of the class remember the size of a unit of measurement". See Memorable Measures below for the printable resources. This activity provides an association with a unit, a visual aid and a known person which is a great memory enhancer.
Mental Methods
Though using pencil and paper are as useful as having up-to-date technology skills, there is no substitute for strategic mental methods for working out calculations and solving problems. The activities in this topic are designed to improve pupils' abilities to use their brains.
Calculating 'in your head' can be a difficult task. If you cannot remember what you have worked out or simply do not know how to solve a problem then it can be very challenging and frustrating. It is important to learn and practise mental arithmetic and using mathematical patterns, you can dramatically improve the speed and accuracy of your mental mathematics.
See also the Arithmetic topic and our Number Skills Inventory.
Mixed
A healthy mashup of activities and ideas to use and apply mathematical knowledge in a variety of situations.
The ultimate customisable lesson Starter is Refreshing Revision. You can choose which topics are included and every time the page is loaded the numbers used in the questions are randomised.
Money
For many pupils the ability to understand financial transactions is a skill they thank their mathematics teacher for. Understanding the use of money is a real, practical application of mathematics in the real world and is just as important today as ever it was.
When it comes to managing our money and avoiding costly mistakes it is well worthwhile to strive to become an expert. There are key aspects of personal finance the pupils should understand as the get older and more independent in their lives and the activities provided here provide resources for a small part of their learning process.
Multiple Intelligences
See also Thinking Skills.
The theory of multiple intelligences was proposed by Howard Gardner in 1983 as a model of intelligence that differentiates intelligence into various specific modalities rather than seeing it as dominated by a single general ability.
Gardner argues that there is a wide range of cognitive abilities, and that there are only very weak correlations among them. For example, the theory predicts that a child who learns to multiply easily is not necessarily generally more intelligent than a child who has more difficulty on this task. The child who takes more time to master simple multiplication:
1) may best learn to multiply through a different approach,
2) may excel in a field outside of mathematics, or
3) may even be looking at and understanding the multiplication process at a fundamentally deeper level, or perhaps as an entirely different process.
Here are some mathematical activities that call upon a pupil's multiple intelligences.
Negative Numbers
A negative number is a real number that is less than zero. Such numbers are often used to represent the amount of a loss or absence. For example, a debt that is owed may be thought of as a negative asset, or a decrease in some quantity may be thought of as a negative increase. Negative numbers are also used to describe values on a scale that goes below zero, such as the Celsius and Fahrenheit scales for temperature.
Here are some activities designed to strengthen a pupil's understanding of negative numbers.
Number
Spotting patterns is an important skill in many areas of life. The world of numbers contains many fascinating patterns and understanding them enables better problem solving strategies. From seeing patterns in the multiples of numbers shaded in a hundred square to spotting the recurring sequences of digits in decimal numbers there is a great deal for pupils to be introduced to.
This topic includes even, odd, prime, triangular, perfect, abundant, square and cube numbers. It uses factors and multiples to find solutions to real life problems and encourages number connections to be investigated for pleasure. There are a lot of puzzles, challenges and games too.
See also the Mental Methods topic and our Number Skills Inventory.
Percentages
Percentages provide a useful and common way to express a part of a quantity. The word is derived from the Latin per centum meaning “by the hundred”. Although percentages are usually used to express numbers between zero and one, any ratio can be expressed as a percentage.
Pupils begin working with common percentages such as 50%, 25% and 10% and practise estimating percentages to get a better understanding of the concept. They then learn how to convert percentages to decimals and vulgar fractions and vice versa.
More advanced problem solving may include percentage change and how it is applied in real life to discounts and interest. A study of the use of percentages in the media can provide many discussion points and can provide a stimulus for classroom display work.
Place Value
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations (such as Roman numerals) for its use of the same symbol for the different orders of magnitude (for example, the "ones place", "tens place", "hundreds place"). This greatly simplified arithmetic and led to the quick spread of the notation across the world.
Probability
Probability is a measure of the weight of evidence, and is arrived at through reasoning and inference. In simple terms it is a measure or estimation of likelihood of the occurrence of an event. The word probability comes from the Latin word probabilitas which is a measure of the authority of a witness in a legal case. Some of the earlier mathematical studies of probability were motivated by the desire to be more profitable when gambling. Today however the practical uses of probability theory go far beyond gambling and are used in many aspects of modern life.
We believe that even adults can, in many cases, have a poor intuition regarding the effects of probability. These activities are designed to help pupils calculate but also get a 'feel' for the principles of probability.
Problem Solving
What good is being a master of calculation if you cannot apply your skills to problem solving? This topic provides lots of examples, activities and situations in which pupils can practise their problem solving skills.
Proof
A mathematical proof is a sequence of statements that follow on logically from each other that shows that something is always true. Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases.
Puzzles
Engaging and addictive, puzzles have been an irresistible lure for inquisitive minds throughout history. This topic introduces pupils to some interesting puzzles with a mathematical connection.
Some puzzles are based on the old classics but are presented in an interactive way or updated to relate to young people of today. The puzzles are recommended to start a lesson, to be used with pupils who finish classwork early or, even better, to be integrated into the main activity of the lesson as strategies for finding solutions are sound mathematical techniques.
A page designed for pupil to access containing the Transum puzzle collection can be found here: Maths Puzzles.
Pythagoras
Pythagoras was a Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. He is most famous for his theorem connecting the lengths of the sides of right angled triangles.
His theorem states that the squares of the lengths of the two shorter sides of any right-angled triangle will add up to the square of the length of the longest side (the hypotenuse).
This theorem can be used to calculate the length of any side of a right-angled triangle if the lengths of the other two sides are known.
Do you know when the next Pythagorean Day is? It will occur when the square of the day added to the square of the month equals the square of the last two digits of the year.
Ratio
A ratio is a relationship between two numbers of the same kind. In layman's terms a ratio represents, simply, for every amount of one thing, how much there is of another thing.
This topic presents a number if different ways pupils can represent ratios and apply their meaning to problem solving situations.
Riddles
A general definition of the word riddle is a statement, question or phrase having a double or hidden meaning and is usually presented as a puzzle to be solved. Posing riddles is an old and respected way of describing mathematical situations, connections and problems.
You will find a number of different types of riddles here which are designed to capture the pupils' interest in a mathematical skill, concept or topic.
Roots
Pupils should learn how to find real roots associated with integer powers (square root, cube root and higher). They should also learn to distinguish between exact representations of roots and their decimal approximations. Just how do you find the cube root of a number? By trial and improvement, iterative calculations or by learning to use a calculator efficiently?
Rounding
The objective of rounding is often to get a number that is easier to use, at the cost of making it less precise. This approximation is very important in dealing with answers to mathematical problems and making them relevant to the real world. Rounding to a given number of decimal places or significant figures is required of pupils.
See also the "Approximating" Starters.
Once the principles of rounding have been understood, a fun way to practise the skills is to play "Rounding Snap".
Sequences
A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them.
The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms.
Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom.
Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.
Sets
Understand the terminology of sets and the basic set operations. Learn about Venn diagrams and the use of sets in the real world.
Shape
This topic is aimed at the learners of basic geometry, which is the study of size, shape and position. More than other areas of mathematics this topic helps pupils to learn about the definitions and properties of basic shapes.
There are many activities provided ranging from simple shape naming games to applying more advanced formulas and theorems. The most popular activities however are those involving pupils to count the number of triangles or rectangles in patterns and come up with effective strategies and justifications for their answers.
The work pupils produce for this topic can make very good display material. The use of colour can enhance the diagrams and make the learning environment more conducive to study. There are many connections between the mathematics of shape and Art. There are fascinating works of art based on symmetry, tessellations and transformations.
Shape (3D)
A particular skill is required to be able to excel in this area of Mathematics. Spatial awareness is important for solving multi-step problems that arise in areas such as architecture, engineering, science, art, games, and everyday life. Children have varying abilities visualizing three dimensional relationships but these abilities can be developed through practical activities and working through mathematical problems. Breaking down three dimensional situations into smaller two dimensional parts in an important strategy for problem solving.
See also the "Shape" Starters.
Simultaneous Equations
This topic covers simultaneous equations with two different variables. The starters pose real world problems which can be solved using the techniques taught at school or by other intuitive methods.
Though there are many formal strategies for solving simultaneous equations the skill of forming the equations from real life situations is a very important stage in working towards a solution.
Algebraic methods are the most efficient for solving basic simultaneous equations but graphical methods, probably using a graphic display calculator or computer software package, may be more suitable for less standard sets of simultaneous equations.
Statistics
Statistics is the study of the collection, organisation, analysis, interpretation and presentation of data. It deals with all aspects of data, including the planning of data collection in terms of the design of surveys and experiments. It also includes describing mathematical relationships between variables and presenting these to an audience in a way that best conveys meaning.
See also the topics called Data Handling, Probability and Averages.
Symmetry
This topic covers line symmetry and rotational symmetry. The innate appeal of symmetry can be found in our reactions to finding symmetry in natural objects, such as precisely formed crystals or seashells. Symmetry in art is another source of delight.
Understanding the mathematics of symmetry is the focus of this topic. Accurately drawing the reflection of an object requires an understanding of the relative positions of reflected points. Defining the position of the mirror line is important to find the position and orientation of the reflection.
The Wrapping Paper lesson starter makes it clear that for rotational symmetry, the position of the centre of rotation is very important.
Work on this topic can produce some excellent display work!
Tables
Times Tables is the common term referring to the multiples of numbers 2 to 12 (or 2 to 10). Having a quick recall of these tables is an important pre-requisite for studying other aspects of mathematics and for coping with personal finance and other area of everyday live involving numbers.
People of any age can improve their skills in recalling table facts. They should learn then as they would learn a song or a dance. You need to know your times tables forwards, backwards and all mixed up. Spend time learning them well and you'll reap the benefits in future.
Here on this website we have developed many activities that help pupils learn their times tables and as then revise them in different ways so that the recall becomes easier and easier. Some of the activities are games and quizzes while others help pupils spot the patterns in the times tables in many different ways.
Here's a plan for learning a new times table in only five days!
Time
This topic provides opportunities for pupils to practise the calculations that are required in time based problems. After mastering the decimal system manipulating units of time can prove to be very difficult for many.
Of all the mathematics topics studied in school this is one of them that has a real and direct practical use in real life. Everyone is more able to cope with day to day tasks if they can read an analogue clock, interpret the 24 hour clock and understand the calendar.
When planning to improve pupils’ estimation skills don’t forget to include practice in estimating time. An amusing diversion in a lesson is to ask everyone to stand up, close their eyes then to sit down when they think a minute has passed.
An fascinating open-ended investigation would be to consider the impact decimal time may have on us all. How would it work, what would need to change and what advantages would it bring?
Transformations
A transformation in mathematics is an operation performed on a shape (or points) which changes the view of that shape (or points). This topic includes four transformations namely reflection, translation, rotations and enlargement.
A reflection can best be described as the mirror image of a shape in a given line (which acts as the mirror). After reflection the shape remains the same size but the orientation is the mirror image of the original.
The transformation known as a translation can be thought of as a movement or shift in position. The size and orientation of the shape remains the same but the position on the plane changes.
A rotation can be described as turning. This transformation is defined by the angle of turning and the centre of rotation (the point which does not move during the turning).
Finally enlargement is the term we use when a shape increases in size but maintains the same shape. The shape after enlargement is defines as being similar to the shape before enlargement. His use of the word similar has a precise mathematical meaning. All of the angles in the enlarged shape are the same as the angles in the original shape and the lengths of the sides are in the same proportion. An enlargement is defines by the scale factor of the enlargement and the centre of enlargement. We use the term enlargement even if the shape becomes smaller (a scale factor between minus one and one). A negative scale factor will produce an enlarged mirror image of the original shape.
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Pupils begin by learning the names on the sides of a right-angled triangle relative to the angles. They then learn the ratios of the lengths of these sides and the connection these ratios have with the size of the angles.
Having mastered right-angled triangle trigonometry pupils then progress to more advanced uses including the sine rule and cosine rules.
The use of a scientific or graphing calculator is essential for this topic and correct, efficient use of the calculator is an important skill to develop.
Here's a Trigonometry Wordsearch just for fun.
Vectors
Vectors usually first make an appearance when pupils learn about transformations. A translation is best described with a vector written as a two by one matrix. Following that pupils learn how vectors can be used to prove geometric relationships in simple line diagrams. Ultimately vectors are studied as a major topic for A Level and International Baccalaureate courses where vectors in three dimensions are included.
You can think of a vector as what is needed to 'carry' the point A to the point B. The Latin word vector means ‘carrier’ and was first used by 18th century astronomers investigating planet rotation around the Sun.
Vocabulary
Mathematics is a language but we also need to understand the language that describes mathematical concepts and techniques.
There are a number of lesson starters and interactive activities that are based around words. The words used are words that pupils will come across in their study of mathematics. By doing these activities pupils will become more familiar with those words, learn how to spell them and dispel misconceptions in some cases.
These activities also provide variety in the study of mathematics and the word games can provide fun and motivation during lessons.
Be aware that even amongst the English speaking nations there can be variations used with the way words are spelled, pronounced and applied but understanding this is all part of education. In an attempt to provide consistency on the Transum Website I am developing this Style Guide.
Xmas
Christmas activities make those December Maths lessons interesting, exciting and relevant. Whether mathematical activities are presented in a Christmas themed way or, due to the festive mood, normal mathematics learning is replaced with puzzles, games and seasonal fun, you can be sure that we have some excellent ideas for you here on the Transum website.
That last week of term before the Christmas holiday is the perfect time to ensure that pupils develop a delight in mathematics by seeing it in an exciting, enjoyable and engaging way (more exciting, enjoyable and engaging than the rest of the term that is!).
In addition to our Christmas activities see also our huge collection of Fun Maths games, puzzles and challenges.
See also our collection of Quick Starters, Random Starters, Substantial Starters and Advanced Starters,


