Xmas Tree Trim
Use the lights provided to decorate each of the Christmas trees so that no two trees are the same.
Ice-cream Combinations
How many two-scoop ice creams can you make from the given flavours?
Misfits
A Misfit is a character with a head, body and legs. How many different Misfits can you create?
Snake Sort
Sort the coloured snakes in a logical order. This activity introduces systematic listing.
Striped Sweets
Learn how to be systematic by colouring the sweet wrappers so that no two are the same.
How Many Triangles?
A self marking step by step approach to calculating the number of triangles in a design.
Six Keys
Use just six keys on your calculator to make a given total. How many different ways can it be done?
Triplets
Find as many sets of three of the available numbers as possible which add up to the given total.
Systematic Listing
Apply systematic listing strategies to find the number of combinations and permutations of choices.
Take Baht
How many different ways can you make a given total with Thai coins?
Scouts in Boats
Arrange a rota for the Scouts to travel in boats so that they are with different people each day.
Egg Box Investigation
In how many different ways can two eggs be arranged in an egg box?
Design a badge
How many different badges can you make using three different coloured squares put together to make a rectangle?
Transum Club
How many different colour schemes can you devise for the Transum Club Badge.
Traffic Jams
How many ways can three cars be lined up in a traffic jam?
House Painting
The houses in Mathsland are all three storeys tall. Each storey is painted using one colour. How many ways can the houses be painted?
Odd Dice
Take three dice. How many ways can they be turned so that they show only odd numbers on top?
This is the main Transum help video on Combinations.
Listing Strategies
Making a list in a logical order will help you avoid repetition and omission when finding combinations and permutations.
Permutations
A video lesson on Permutations, calculating them using the counting principle and the nPr formula.
Combinations and Permutations
Learn how to tell the difference between permutations and combinations and use the formulae to answer questions.
The Counting Principle
The Counting Principle, Permutations, and Combinations. A fast paced, clearly illustrated video.
Ice-cream Combinations
How many two-scoop ice creams can you make from the given flavours?
Snake Sort
Sort the coloured snakes in a logical order. This activity introduces systematic listing.

Bus Stop
How many different ways can four people stand in line?

How Many Squares? 2
How many squares can be found by joining four dots on the grid?

How Many Triangles? 1
How many Triangles can you find in the diagram?

How Many Triangles? 2
How many triangles are hidden in the pattern? What strategy might you use to count them all to ensure you don't miss any out?
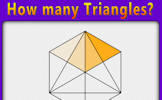
How Many Triangles? 3
Find a systematic way of counting the number of triangles in the given diagram.

Ice Cream
How many different ice cream cones can be made by choosing two scoops from six flavours?

Noughts and Crosses
In how many different ways can the first X and O by placed on the grid?

Snowman and Woman
How many different ways can you spell out the word snowman by moving from snowflake to snowflake.

Thai Baht
How many different ways can you make a given total with Thai coins?

Tran's Hats
In how many different ways might Tran decide to wear his hats in one week?
31 items are currently in this category.
Teachers might find the complete Combinations Topic List useful.
"A combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange." - Wikipedia
In Primary school pupils should practise sorting and grouping items noting similarities and differences. They should develop strategies for finding all the ways a small number of items can be arranged so that missing or duplicates can be found quickly.
By the end of Secondary school pupils will have learnt the formulas for combinations and permutations and apply them when solving probability problems.