Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of May 2025. It begins, as usual, with the puzzle of the month.
Freddie returned a defective Bluetooth speaker to the shop and asked for his money back. By mistake, the shop assistant reversed the pounds and pence in the refund: the amount of pence was given as pounds, and the pounds were given as pence. Freddie did not notice and put the money in his pocket.
On his way home, he used £1.50 from the money in his pocket to buy a drink. When he got home, he counted the money left in his pocket and found he had exactly twice as much as the cost of the speaker.
What was the cost of the speaker?

If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email at gro.musnarT@rettelsweN
While you think about that, here are some of the key resources added to the Transum website during the last month.
Pythagoras with Surds. This new three-level exercise was suggested by subscriber Sharon, way over there in Beijing. As the title suggests, each question requires Pythagoras' Theorem to find a solution which must be written as a simplified surd (or radical).
Two Measures is a new three-level exercise. It takes two rulers to measure a pencil and that's only the first question of level 1. By the time you get to level 3 you'll be wondering how those elementary-school children in China figured out the height of their table with the help of a cat and a tortoise.
Problems Leading To Quadratics is a brand new exercise designed for those who have already mastered the methods for solving quadratic equations. There are a total of 30 questions presented in a three-level, self-marking exercise. There is a theme connecting all of the questions; they are all taken from an 1885 textbook though the English has been updated for a present day reader. The contexts add interest to the questions and by the time you reach Level 3 you wonder how those nineteenth century learners managed!
I have started collecting Hidden Gems - my name for some activities on the website that you may not have come across before. They are activities that do not necessarily fit into a particular topic, but I feel they are very worthwhile nonetheless. They are all related to some mathematical concept and each one of them has worked well with my students at some point. Click the image below and have a look!
The Recurring Decimals exercise now has a third level. Inspired by the comment from Ann that you can see underneath the exercises. Level 3 invites learners to distinguish between terminating and recurring decimal equivalents by considering the prime factors of the denominators of the fractions reduced to their lowest forms. It's actually much easier than that last sentence suggests!
The month of May usually signals the beginning of the exam season for many. Here are some revision resources you may like to pass on. In the Northern hemisphere the weather is expected to improve relative to its previous performance. You might find it possible to do some Outdoor Maths. The first of May has a calendar-related Starter called May Day and the 4th of May, for those of a certain age, is Star Wars Day.
🌨️☁️🌞⛅🌤️⛅🌞☁️🌨️
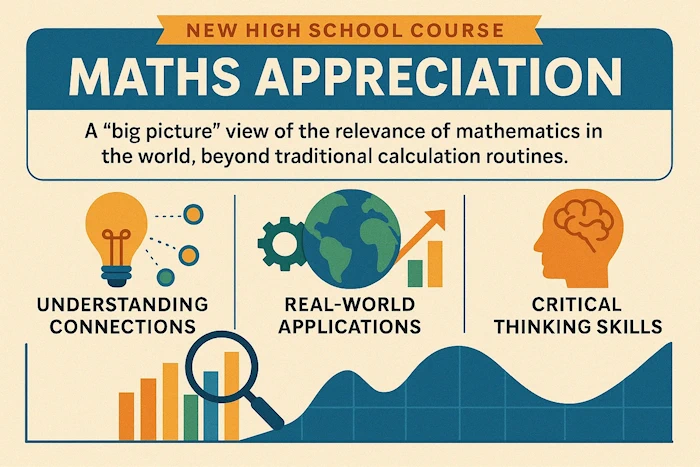
As you may remember, I enjoy listening to podcasts. In a recent episode of Tim Harford's Cautionary Tales podcast, an intriguing conversation with Freakonomics co-author Steven Levitt touched on the concept of "Maths appreciation" courses. Similar to how art appreciation classes teach students to understand and discuss artwork without necessarily creating it themselves, Levitt suggested that students who may not become mathematicians could still benefit from understanding how maths and data work in the real world. This approach could help students see the relevance and beauty of mathematics even if they don't engage with complex calculations.
Particularly noteworthy was their discussion about young people aged 12-13 who often decide they're 'not maths people' and mentally check out of mathematical learning. The podcast highlighted how this critical age represents a turning point where many students disengage because they don't understand the purpose behind the complex mathematics they're learning.
Don't forget you can listen to this month's Transum podcast, which is the audio version of this newsletter.
Four days ago, just before 12:16 p.m. April 27, 2025, it was time for my annual check that the sun is obeying the rules! The sun is directly overhead so there are no shadows from the cans (my three-can test) in my photograph below. It's Bangkok's 'Zero-Shadow Day' but why doesn't it occur at noon?

According to my trusty AI friend:
I hope I'm not the only person who has never previously heard of the 'Equation of Time'!
Of course no shadows are also attributed to vampires, witches and Peter Pan but three cool drinks are far preferable.
Finally, the answer to last month's puzzle which was:
I paid £3.60 for the mini Easter eggs I bought from the corner shop. The shop owner added two extra eggs because the best-before date was rapidly approaching. That brought the total cost down by 30p per dozen compared to the original price.
How many eggs did I buy?
The answer is 16. Some solution methods can be found below.
This puzzle was adapted from a similar puzzle posted on the James Madison University website.
The first five people to solve the puzzle were Kevin, Chris, Rick, Mala and Esther. Thanks to everyone who took part. Good luck with this month's puzzle.
That's all for now.
John
P.S. Why doesn't the world of whole numbers trust primes?
Because they make up everything.
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Chris, Scotland
Tuesday, April 1, 2025
"Let the initial number of eggs = E
The price per dozen eggs is 3.60/(E/12) or 43.20/E
The new price per dozen is given by 43.20/(E+2) but we're told this is 30p less than the previous price per dozen so:
43.20/(E+2) = 43.20/E - 0.30
43.20E = 43.20(E+2) - 0.3E(E+2)
144E = 144(E+2) - E(E+2)
144E = 144E + 288 - E^2 -2E
E^2 + 2E - 288 = 0
(E+18)(E-16)=0
E = -18 or E =16
Obviously only E = 16 is valid for this question.
Initially, it was 16 eggs for £3.60 which is £2.70 per dozen.
With the extra two eggs it was 18 eggs for £3.60 which is £2.40 per dozen (30p cheaper)."
Rick,
Wednesday, April 2, 2025
"First, being American and used to dollars, I assume that 30p = £0.30.
Let D equal the number of dozen eggs purchased.
3.60 / D = 3.60 / (D + 1/6) + 0.30, where 1/6 represents the number of additional eggs (as a fraction of a dozen).
Multiplying both sides of the equation first by (D + 1/6) and then by D results in a quadratic equation. Then factoring resulted in two solutions, one positive and one negative. The positive solution was 4/3, or 16 eggs. "
Mala, New Zealand
Sunday, April 6, 2025
"The answer is: I bought 16 eggs.
Price per dozen for x eggs= 3.60/(x/12)
Price per dozen of x+2 eggs = 3.60/(x+2/12)
Since the difference is 0.30, the quadratic equation gives the value of x =16."