Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of July 2023. It begins, as usual with the puzzle of the month.
x + xy + y = 90
If x and y are positive integers, what is the sum of x and y?
While you think about that here are some of the key resources added to the Transum website during the last month.
The Integration exercise now has new levels, worked solutions and help video. The new levels cover integration by substitution and integration by parts.
The Common Trig Ratios exercise was originally written in degrees but it now has a companion set of exercises in radians. Thanks Angus for the suggestion.
It's my birthday in July! I'll no longer be both a square and a cube but I will be the product of two prime numbers (see place-valued cakes below)! If you would like to know the date of by birthday (so that cards and presents can arrive at the right time) you can find clues on the newly created Happy Birthday page.
While putting together the birthday activities I finally learnt the method for calculating the day name of any date this century (The Doomsday Algorithm). It's a skill I've long admired in others. Have a look at my step-by-step instructions and you could be a date genius too!
For many of you, the school year concludes in July. As always I hope those last few lessons and the holidays are used to expose your students to some exciting, interesting and extraordinary mathematical activities such as these:
|
End of Term Maths
Wouldn't it be sad if those last Maths lessons of the Term were wasted. Quite often special school activities take place during the last week of Term and as a result some pupils are taken out of normal lessons leaving you, the teacher with only two thirds of your normal class and an expectation to do something different. It would be a crime if you put on a video (unless it was a Maths video) or simply told the pupils to get on with their own pastimes when there are so many out-of-the-ordinary mathematical activities you could be doing. Click here to see hand-picked selections of activities that have worked for me in the past and would be great fun for you to try with your classes at the end of this Term. |
School Holiday Activities
Students are encouraged to continue their learning during the holidays. Research indicates that by the end of the long summer holiday pupils perform, on average, one month behind where they left off in the spring. Here are some suggestions for activities that will keep children thinking mathematically while having fun and learning new skills. You can give a link to this page to all of your pupils and even if only half a dozen of them take up the challenge that’s better than nothing. Let me know if you have other ideas. |
The Starter of the Day for 4th July is themed on American Independence Day. It’s ironic that most of the American students who might appreciate the reference won’t be in school on that day so won’t see it!
Continuing the trend in the last few newsletters of letting you know of my experience of using artificial intelligence - this month I have been using the ChatGPT plugins Wolfram and Show My Diagrams. I asked it to gather the data then produce a bar chart showing the frequencies of the first digit of country populations (an example of Benford's Law):
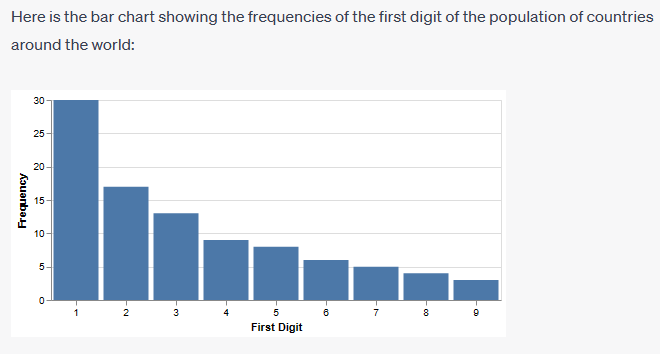
I then found myself in a conversation with this artificial intelligence about how Benford's Law is counter-intuitive because it predicts that one will be the leading digit about 30% of the time, while nine will be the leading digit only about 5% of the time. This is contrary to the uniform distribution that many people might expect, where each digit from one to nine would have an equal chance of being the leading digit. It is also interesting to note that the law applies regardless of the unit of measurement. So, whether a country's population is measured in thousands, millions, or billions, the distribution of leading digits should still follow Benford's Law.
Did you know that Benford's Law is used in forensic accounting and fraud detection because when people make up numbers, they often fail to follow the distribution predicted by Benford's Law. This can be a red flag for investigators.
I then starting thinking if this would make a suitable topic for internally assessed coursework. What other demographic data follows Benford's Law (e.g., age distributions, income levels, etc.)?
Talking of populations, the 11th July is World Population Day and is highlighted with the Starter called Absolutely Everyone. That counter has long passed the eight billion mark and continues to increase. This Starter allows you to choose your own questions that might be accessible to your students.
Asking for a friend ... Weight is continuous data. If weights are collected to the nearest integer is the collected data now discrete? What is the range of the data in the table below?
Thought I should include the following photograph of a paper construction that my nonagenarian mother made at her fortnightly ladies group meeting. I have also added it to the Paper Constructions page.
Don't forget you can listen to this month's podcast which is the audio version of this newsletter. You can find it on Spotify, Stitcher or Apple Podcasts. You can follow Transum on Twitter and 'like' Transum on Facebook. If you have any comments about this podcast please contact me at podcast@transum.org.
Finally the answer to last month's puzzle which is negative one half. As a reminder here is the puzzle:
x squared equals sixteen to the power of x. Find the value of x.
Congratulations to Pauline Johnson, Chris Smith, Rick Blair, Kate Cooper Nigel Fern for being the first five to let me know they had solved the puzzle.
I initially simplified the equation by finding the square root of both sides but then when I failed to find a solution algebraically I resorted to using the graph plotter to find the root of \(y=x^2-16^x\). Did you have a better, more elegant method?
A trial-and-improvement (iterative) method would have also worked. Rick told me "I used logic, to eliminate positive and negative numbers greater than one and positive fractions., leaving negative fractions. Using the first negative fraction of one half solved the problem, so I stopped."
That's all for now,
John
P.S. Calendars, their days are numbered.
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
