Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Tree Diagram Creator Quickly create a probability tree diagram to use as a visual aid.
Tree Diagram Creator Quickly create a probability tree diagram to use as a visual aid.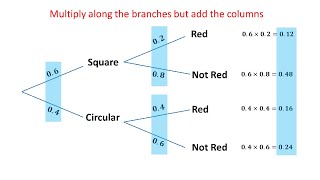 Tree Diagrams Video Tree diagrams can be really helpful showing combinations of two or more events in order to calculate probabilities.
Tree Diagrams Video Tree diagrams can be really helpful showing combinations of two or more events in order to calculate probabilities.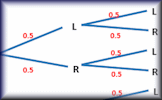 Tree Diagrams Calculate the probability of independent and dependent combined events using tree diagrams.
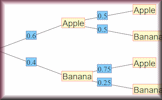
Tree Diagrams Calculate the probability of independent and dependent combined events using tree diagrams.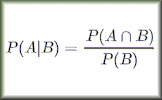 Conditional Probability Find the probability of one event happening given that another event has already happened.
Conditional Probability Find the probability of one event happening given that another event has already happened.
Here are some exam-style questions on this statement:
- "A driving test has two sections, practical(p) and theory(t). One day everyone who took the test passed at least one section. 77% passed the practical section and 81% passed the theory section." ... more
- "Twenty nine children went to a zoo to photograph some animals. The numbers of children who photographed Lions(L), Monkeys(M) and Zebras (Z) are given as follows:" ... more
- "Neal is attending a Scout jamboree in Japan. He has both boots and trainers to wear. He also has the choice of wearing a cap or not." ... more
- "The time in minutes taken to drive through a city at different times of the day can be modelled by a normal distribution with mean of 45 and standard deviation of 12. A commuter will be late for work if it takes more than an hour to drive through the city." ... more
- "Events \(A\) and \(B\) are such that \(P(A) = 0.25\), \(P(A|B) = 0.15\) and \(P(A \cup B) = 0.65\)." ... more
- "Julie chooses a cake from a yellow box on a shelf. The box contains two chocolate cakes and three plain cakes. She eats the cake and chooses another one from the box. The tree diagram below represents the situation with the four possible outcomes where C stands for chocolate cake and P for plain cake." ... more
- "Jane and David play two games of golf. The probability that Jane wins the first game is \(\frac56\). If Jane wins the first game, the probability that she wins the second game is \(\frac67\)." ... more
- "A factory manufactures switches. It is known that the probability that a switch is found to be defective is 0.04. A random sample of 50 switches is tested." ... more
- "At a fitness club, \( 60\% \) of the members are full-time members, and \( 30\% \) of the members participate in group fitness classes. \( 25\% \) of the members are neither full-time members nor participate in group fitness classes." ... more
- "The weights of players in a sports league are normally distributed with a mean of 75.2 kg, (correct to three significant figures). It is known that 75% of the players have weights between 67 kg and 80 kg. The probability that a player weighs less than 67 kg is 0.05." ... more
- "Eels are elongated fish, ranging in length from 5cm to 4m. In a certain lake the length of the eels are normally distributed with a mean of 84cm and a standard deviation of 18cm. Eels are classified as giant eels if they are more than 120 cm long." ... more
- "Two events A and B are such that \(P(A) = 0.57\) and \(P (A \cap B) = 0.21\)." ... more
Here are some Advanced Starters on this statement:
- Airport Security
The old lady has a misconception about conditional probability more - Bertrand's Box Paradox
Bertrand's box paradox is a paradox of elementary probability theory, first posed by Joseph Bertrand in 1889 more - Other Child's Gender
What is the probability that the other child is also a boy? more - Two Pots
Use tree diagrams to find the surprising result that probabilities of different situations are the same. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
In probability theory, the concept of conditional probability is pivotal in determining the likelihood of an event given that another event has occurred. The formal definition is expressed by the formula \( P(A|B) = \frac{P(A \cap B)}{P(B)} \), where \( P(A|B) \) denotes the probability of event A occurring given that B has occurred, \( P(A \cap B) \) is the probability of both A and B occurring, and \( P(B) \) is the probability of event B. This relationship is crucial for understanding how the occurrence of one event affects the probability of another.
For independent events, where the occurrence of one event does not influence the occurrence of another, the conditional probability formula simplifies. If events A and B are independent, then \( P(A|B) = P(A) \) and \( P(A \cap B) = P(A) \times P(B) \), showing that the probability of A occurring given B has occurred is simply the probability of A occurring. The formulas are key in identifying whether events influence each other or can be considered independently.
Key Formulas:
Conditional Probability: \( P(A|B) = \frac{P(A \cap B)}{P(B)} \)
Independence: \( P(A|B) = P(A) \) and \( P(A \cap B) = P(A) \times P(B) \)
Formal Definition:
A and B are independent events if the occurrence of each one of them does not affect the probability that the other occurs.
This means that $$P(A \mid B) = P(A \mid B') = P(A)$$ and that $$P(B \mid A) = P(B \mid A') = P(B)$$.
Example:
Let's consider two events, A and B, within a standard deck of 52 playing cards. Event A is drawing an ace, and event B is drawing a heart. To find the probability of drawing an ace given that we have drawn a heart, we use the conditional probability formula:
$$
P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{52}}{\frac{13}{52}} = \frac{1}{13}
$$
This result tells us that if we know a heart has been drawn, there is a 1 in 13 chance that it is also an ace.

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

