Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Mix and Math Determine the nature of adding, subtracting and multiplying numbers with specific properties.
Mix and Math Determine the nature of adding, subtracting and multiplying numbers with specific properties. Identity, Equation or Formula? Arrange the given statements in groups to show whether they are identities, equations or formulae.
Identity, Equation or Formula? Arrange the given statements in groups to show whether they are identities, equations or formulae.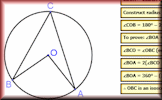 Proof of Circle Theorems Arrange the stages of the proofs for the standard circle theorems in the correct order.
Proof of Circle Theorems Arrange the stages of the proofs for the standard circle theorems in the correct order.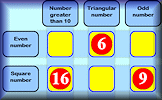 Satisfaction This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers.
Satisfaction This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers.
Here are some exam-style questions on this statement:
- "State whether each of the following statements is true or false. Give reasons for your answers." ... more
- "One is added to the product of two consecutive positive even numbers. Show that the result is a square number." ... more
- "(a) Give a reason why 0 is an even number." ... more
- "Betsy thinks that \((3x)^2\) is always greater than or equal to \(3x\)." ... more
- "Given that \(n\) can be any integer such that \(n \gt 1\), prove that \(n^2 + 3n\) is even." ... more
- "Use algebra to prove that \(0.3\dot1\dot8 \times 0.\dot8\) is equal to \( \frac{28}{99} \)." ... more
- "The diagram shows a quadrilateral ABCD in which angle DAB equals angle CDA and AB = CD." ... more
- "m and n are positive whole numbers with m > n" ... more
- "(a) Prove that the recurring decimal \(0.\dot2 \dot1\) has the value \(\frac{7}{33}\)" ... more
- "Express as a single fraction and simplify your answer." ... more
- "(a) Prove that the product of two consecutive whole numbers is always even." ... more
- "The number \(T\) can be expressed as \(T = 4k + 3\) where \(k\) is a positive integer." ... more
- "Consider the sum of the squares of any two consecutive odd integers." ... more
- "Prove that the integers \(a\) and \(b\) cannot both be odd if \(a^2+b^2\) is exactly divisible by 4." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Example, Show that the algebraic generalisation of the following is true.
$$ \frac{1}{m+1} + \frac{1}{m^2+m} \equiv \frac{1}{m} $$Let's start by finding a common denominator for the left-hand side of the equation:
$$ \frac{1}{m+1} + \frac{1}{m(m+1)} $$ $$ \frac{m + 1}{m(m+1)} $$Now, let's simplify the expression:
$$ \frac{1}{m} $$It is now evident that the original equation:
$$ \frac{1}{m+1} + \frac{1}{m^2+m} \equiv \frac{1}{m} $$Is generally true, as the left-hand side simplifies to \( \frac{1}{m} \).
Thus, the algebraic generalisation provided does hold true for all values of \( m \).
Proof: Irrationality of \( \sqrt{3} \) and \( \sqrt[3]{5} \)
Statement: (a) The square root of 3 is irrational. (b) The cube root of 5 is irrational.
Proof (a): Irrationality of \( \sqrt{3} \)
Let's prove by contradiction. Assume that \( \sqrt{3} \) is rational.
Then, \( \sqrt{3} \) can be expressed as a fraction \( \frac{p}{q} \) where \( p \) and \( q \) are coprime integers (i.e., their greatest common divisor is 1) and \( q \neq 0 \).
\[ \sqrt{3} = \frac{p}{q} \]
Squaring both sides:
\[ 3 = \left( \frac{p}{q} \right)^2 \]
\[ 3q^2 = p^2 \]
This implies that \( p^2 \) is divisible by 3, so \( p \) must also be divisible by 3. Let \( p = 3k \) for some integer \( k \).
Substitute \( p = 3k \) back into the equation \( 3q^2 = p^2 \):
\[ 3q^2 = (3k)^2 \]
\[ 3q^2 = 9k^2 \]
\[ q^2 = 3k^2 \]
This implies that \( q^2 \) is also divisible by 3, so \( q \) must also be divisible by 3.
However, this is a contradiction because we assumed that \( p \) and \( q \) are coprime, but we have shown that both are divisible by 3. Therefore, \( \sqrt{3} \) must be irrational.
Proof (b): Irrationality of \( \sqrt[3]{5} \)
Let's prove by contradiction. Assume that \( \sqrt[3]{5} \) is rational.
Then, \( \sqrt[3]{5} \) can be expressed as a fraction \( \frac{m}{n} \) where \( m \) and \( n \) are coprime integers and \( n \neq 0 \).
\[ \sqrt[3]{5} = \frac{m}{n} \]
Cubing both sides:
\[ 5 = \left( \frac{m}{n} \right)^3 \]
\[ 5n^3 = m^3 \]
This implies that \( m^3 \) is divisible by 5, so \( m \) must also be divisible by 5. Let \( m = 5l \) for some integer \( l \).
Substitute \( m = 5l \) back into the equation \( 5n^3 = m^3 \):
\[ 5n^3 = (5l)^3 \]
\[ 5n^3 = 125l^3 \]
\[ n^3 = 25l^3 \]
This implies that \( n^3 \) is also divisible by 5, so \( n \) must also be divisible by 5.
However, this is a contradiction because we assumed that \( m \) and \( n \) are coprime, but we have shown that both are divisible by 5. Therefore, \( \sqrt[3]{5} \) must be irrational.
Conclusion: Both \( \sqrt{3} \) and \( \sqrt[3]{5} \) are irrational numbers.
Euclid’s Proof of an Infinite Number of Prime Numbers
Euclid's proof is a classic example of a proof by contradiction. It is found in Euclid's Elements, Book IX, Proposition 20. Here's a simplified version of the proof:
Assumption:
Assume that there are only a finite number of prime numbers, say \( p_1, p_2, p_3, \ldots, p_n \).
Construction:
1. Consider the number \( N \) formed by multiplying all these assumed finite prime numbers together and then adding 1:
$$ N = p_1 \cdot p_2 \cdot p_3 \cdot \ldots \cdot p_n + 1 $$
Contradiction:
2. Now, \( N \) is either prime or composite.
- If \( N \) is prime, then we have found a prime number not in our original list, which is a contradiction.
- If \( N \) is composite, then it must have a prime factor.
3. Any prime factor of \( N \) cannot be one of the primes in our original list because it would leave a remainder of 1 when divided by any of them.
For example, if \( p \) is any prime in the list, then:
$$ N \mod p = (p_1 \cdot p_2 \cdot p_3 \cdot \ldots \cdot p_n + 1) \mod p = 1 $$
4. Therefore, the prime factor of \( N \) is another prime number not in our original list, which is again a contradiction.
Conclusion:
Since the assumption that there are only a finite number of prime numbers leads to a contradiction, we conclude that there must be an infinite number of prime numbers.
This elegant proof demonstrates that no matter how many prime numbers we have, we can always construct a new number that reveals the existence of yet another prime number, thus showing the infinitude of the primes.
Proof: Sum of a Rational and an Irrational Number
Statement: If \( a \) is a rational number and \( b \) is an irrational number, then \( a + b \) is an irrational number.
Proof:
Let's prove this statement by contradiction. We will assume that the sum of a rational number \( a \) and an irrational number \( b \) is rational, and show that this leads to a contradiction.
Assumption:
Assume that \( a \) is a rational number and \( b \) is an irrational number, but \( a + b \) is rational.
By definition, a rational number can be expressed as the quotient of two integers. So, we can write:
\[ a = \frac{p}{q} \]
where \( p \) and \( q \) are integers and \( q \neq 0 \).
Since we are assuming that \( a + b \) is rational, we can write:
\[ a + b = \frac{m}{n} \]
where \( m \) and \( n \) are integers and \( n \neq 0 \).
Contradiction:
Now, let's isolate \( b \) in the equation \( a + b = \frac{m}{n} \):
\[ b = \frac{m}{n} - a = \frac{m}{n} - \frac{p}{q} = \frac{mq - np}{nq} \]
Since the subtraction of two rational numbers is also a rational number, this implies that \( b \) is rational, which is a contradiction because we assumed \( b \) to be irrational.
Conclusion:
Since our assumption that \( a + b \) is rational leads to a contradiction, we conclude that the sum of a rational number \( a \) and an irrational number \( b \) must be irrational.
Proof: Not All Elements of Set P are Prime
Statement: Consider the set \( P \) of numbers of the form \( n^2 + 41n + 41 \) where \( n \) belongs to the set of natural numbers \( \mathbb{N} \). We need to show that not all elements of \( P \) are prime.
Proof:
To show that not all elements of \( P \) are prime, it is sufficient to find one value of \( n \) for which \( n^2 + 41n + 41 \) is not a prime number.
Let's consider the expression:
\[ n^2 + 41n + 41 \]
For a number to be prime, it must be greater than 1 and have no positive divisors other than 1 and itself.
Let’s find a value of \( n \) for which the expression yields a composite (non-prime) number:
Consider \( n = 41 \),
\[ 41^2 + 41 \cdot 41 + 41 \]
\[ 41(41 + 41 + 1) \]
\[ 41(83) \]
Conclusion:
Since \( 41(83) \) is a product of two integers, both greater than 1, it is a composite number. Therefore, we have found a value of \( n \), namely \( n = 41 \), for which \( n^2 + 41n + 41 \) is not a prime number. This demonstrates that not all elements of the set \( P \) are prime.
Counterexample for Integer Solutions
We are given the statement that there are no positive integer solutions to the equation:
$$ x^2 + y^2 = 10 $$To disprove this statement, we need to find at least one pair of positive integers \( x \) and \( y \) that satisfy the equation. A counterexample exists if we can find such a pair.
Let's consider the pair \( (x, y) = (1, 3) \). Substituting these values into the equation gives:
$$ 1^2 + 3^2 = 1 + 9 = 10 $$Since \( 10 = 10 \), the pair \( (1, 3) \) is a solution to the equation, and thus, it serves as a counterexample to the given statement.
Now, let's delve into why this example serves as a counterexample. A counterexample is an example that refutes a statement or proposition. In this case, the statement to be disproven posits that there are no positive integer solutions to the equation \( x^2 + y^2 = 10 \). By finding a pair of positive integers, \( (1, 3) \), that satisfies the equation, we have effectively shown that the original statement is not always true. Hence, the existence of this pair of positive integers serves as a counterexample, disproving the assertion that no such pairs exist.
In conclusion, the statement that there are no positive integer solutions to the equation \( x^2 + y^2 = 10 \) is not always true, as demonstrated by the counterexample \( (x, y) = (1, 3) \).
Transum,
Saturday, August 17, 2019
"Here is a Starter for a lesson on proof:
Write down as many reasons you can think of that prove zero is an even number.
[Subscribers can find some of the ways that zero can be shown to be an even number here.]"
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

