Cookies are used on this website.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

• Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise.
• New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations.
• Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.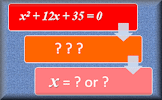
• Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.
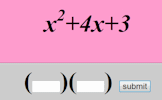• Factorising Quadratics An exercise about factorising quadratics presented one question at a time suitable for a whole class activity.
• Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
• Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level.
• Factorise Any Quadratic What if you could solve any quadratic function without any guess-and-check or memorization? This video shows you how.
• Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.

Here are some exam-style questions on this statement:

• "The volume of the larger red cube is 386cm³ greater than the volume of the smaller blue cube." ... more
• "The diagram shows part of the graph \(y=x^2-3x+6\)." ... more
• "(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\)." ... more
• "In the diagram below, which is not drawn to scale, all dimensions are in centimetres and all angles are multiples of 90^o. If the shaded area is 698cm², work out the value of \(x\)." ... more
• "Given that:" ... more
• "Given that \(x^2 – 8x + 3 = (x – a)^2 – b\) for all values of x," ... more
• "The area of triangle ABC (not drawn to scale) is " ... more
• "If \(y = 5x^4 + 3x^2\) and \(x=\sqrt{w+2}\), find \(w\) when \(y = 12\) showing each step of your working." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

• Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".