|
|
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
The volume of the larger red cube is 386cm3 greater than the volume of the smaller blue cube.
The lengths of the edges of the blue cube can be expressed as \(x\) cm.
The lengths of the edges of the red cube can be expressed as \(x+2\) cm.
(a) Show that \( x^2 + 2x - 63 = 0 \).
(b) Find the volume of the blue cube.
2. | GCSE Higher |
The diagram shows part of the graph \(y=x^2-3x+6\).
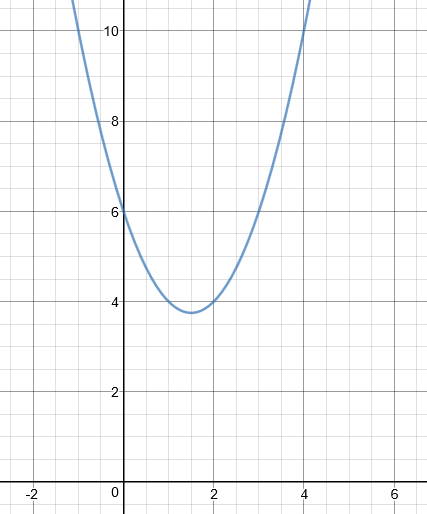
(a) By drawing a suitable straight line, use your graph to find estimates for the solutions of \(x^2 - 4x + 2 = 0\) to one decimal place.
(b) A is the point (2,4). Calculate an estimate for the gradient of the graph at the point A.
3. | IGCSE Extended |
(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\).
(b) Solve the equation \(3x^2-8x-5=0\) showing all of your working and giving answers to three significant figures.
(c) The total surface area of a cone with radius \(x\) and slant height \(8x\) is equal to the area of a circle with radius r. Show that \(r = 3x\).
[The curved surface area, \(A\), of a cone with radius \(r\) and slant height \(l\) is \(A=\pi rl\).]
4. | GCSE Higher |
In the diagram below, which is not drawn to scale, all dimensions are in centimetres and all angles are multiples of 90o. If the shaded area is 698cm2, work out the value of \(x\).
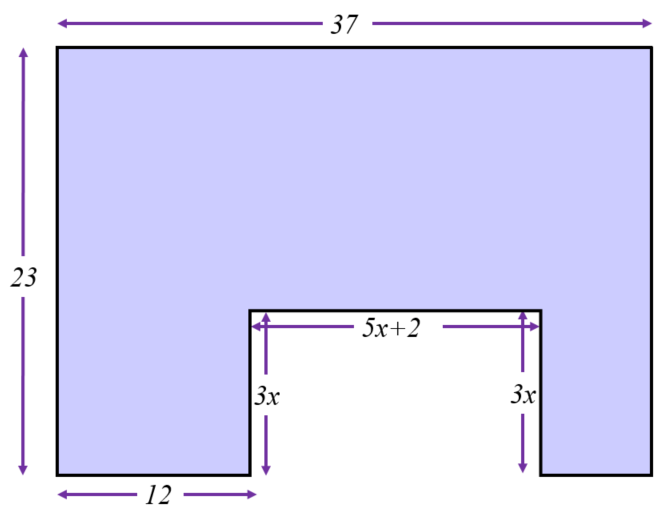
5. | GCSE Higher |
Given that:
$$ x^2 : (5x + 3) = 1 : 3 $$find the possible values of \(x\).
6. | GCSE Higher |
Given that \(x^2 – 8x + 3 = (x – a)^2 – b\) for all values of x,
(a) find the value of a and the value of b.
(b) Hence write down the coordinates of the turning point on the graph of \(y = x^2 – 8x + 3\)
7. | GCSE Higher |
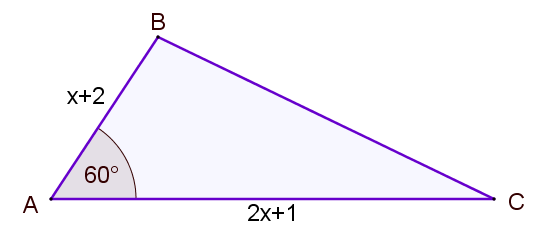
The area of triangle ABC (not drawn to scale) is
$$ \frac{35 \sqrt{3}}{4} m^2$$If AB = \(x+2\) metres and AC = \(2x+1 \) metres, find the value of \(x\).
8. | GCSE Higher |
If \(y = 5x^4 + 3x^2\) and \(x=\sqrt{w+2}\), find \(w\) when \(y = 12\) showing each step of your working.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
