Expanding and factorising
Term 1 starting in week 7 :: Estimated time: 2 weeks
- Expand and factorise with a single bracket (review)
- Expand binomials (review)
- Factorise quadratic expressions
- Solve equations equal to zero
- Solve quadratic equations by factorisation
For higher-attaining pupils:
- Factorise complex quadratic expressions
- Solve complex quadratic expressions by factorisation
- Complete the square Solve quadratic equations using the quadratic formula
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
 Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise.
Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise. New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations.
New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations. Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.
Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.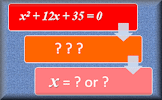 Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.
Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise. Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
Completing the Square Practise this technique for solving quadratic equations and analysing graphs. Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level.
Where am I with Algebra? Find out how developed your algebra skills are and then take them to the next level. Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds. Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.
Using Graphs Use the graphs provided and create your own to solve both simultaneous and quadratic equations.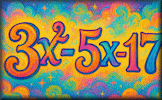 Problems Leading To Quadratics Situations from 1885 which can be described using algebra and explained by solving quadratic equations
Problems Leading To Quadratics Situations from 1885 which can be described using algebra and explained by solving quadratic equations
Here are some exam-style questions on this topic:
- "Write down the coordinates of the turning point on the graph of \(y = 9 - (x - 5)^2\)" ... more
- "The volume of the larger red cube is 386cm3 greater than the volume of the smaller blue cube." ... more
- "The straight line \(y = 3x - 4\) intersects the curve \(y = x^2 + 4x – 7\) at the points \(A\) and \(B\)." ... more
- "The diagram shows part of the graph \(y=x^2-3x+6\)." ... more
- "The graph of y = f(x) is drawn accurately on the grid." ... more
- "(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\)." ... more
- "(a) By completing the square, solve \(x^2+8x+13=0\) giving your answer to three significant figures." ... more
- "The diagram below is a sketch of a curve, a parabola, which is not drawn to scale." ... more
- "In the diagram below, which is not drawn to scale, all dimensions are in centimetres and all angles are multiples of 90o. If the shaded area is 698cm2, work out the value of \(x\)." ... more
- "Given that:" ... more
- "Given that \(x^2 – 8x + 3 = (x – a)^2 – b\) for all values of x," ... more
- "The area of triangle ABC (not drawn to scale) is " ... more
- "(a) Find the interval for which \(x^2 - 9x + 18 \le 0\)" ... more
- "If \(y = 5x^4 + 3x^2\) and \(x=\sqrt{w+2}\), find \(w\) when \(y = 12\) showing each step of your working." ... more
- "(a) Write \(2x^2+8x+27\) in the form \(a(x+b)^2+c\) where \(a\), \(b\), and \(c\) are integers, by 'completing the square'" ... more
- "A function is defined as \(f(x) = 2{(x - 3)^2} - 5\) ." ... more
- "Let \(f(x)=5x^2-20x+k\). The equation \(f(x)=0\) has two equal roots." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson

Arithmagons
This lesson starter requires pupils to find the missing numbers in this partly completed arithmagon puzzle.
2nd Lesson

Lemon Law
Change the numbers on the apples so that the number on the lemon is the given total.
3rd Lesson

Analogies
Make more of analogies to help remember mathematical concepts.
4th Lesson

Big Order
Estimate or calculate then put the large numbers in order of size.
5th Lesson

Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
6th Lesson

Cube Calendar
What numbers should be on each face of the two cubes to make this perpetual calendar?
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.

