Vectors
Term 2 starting in week 5 :: Estimated time: 2 weeks
- Understand and represent vectors
- Use and read vector notation
- Draw and understand vectors multiplied by a scalar
- Draw and understand addition of vectors
- Draw and understand addition and subtraction of vectors
For higher-attaining pupils:
- Explore vector journeys in shapes
- Explore quadrilaterals using vectors
- Understand parallel vectors
- Explore collinear points using vectors
- Use vectors to construct geometric arguments and proofs
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Vector Maze Use vectors to navigate through a maze by the shortest distance.
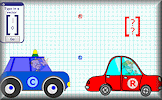Vector Cops Help the cops catch the robbers by finding the vectors that will end the chase.
Vectors Video Learn about addition and subtraction of vectors and multiplication of a vector by a scalar.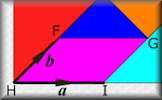
Vectors An online exercise on addition and subtraction of vectors, multiplication of vectors by a scalar, and diagrammatic representations of vectors.
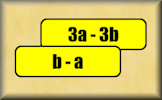Parallel Vectors Collect together in groups the vectors that are parallel to each other.
Here are some exam-style questions on this topic:
- "Find \(4a - b\) as a column vector." ... more
- "Calculate the vector \(3a - 2b\) if the vectors \(a\) and \(b\) are:" ... more
- "OABC is a parallelogram with O as origin. The position vector of A is \(a\) and the position vector of C is \(c\)." ... more
- "(a) Shape \(A\) is translated to shape \(B\) using the vector \( \begin{pmatrix}m\\n\\ \end{pmatrix}\). What are the values of \(m\) and \(n\)?" ... more
- "ABCD is a quadrilateral. The points E, F, G and H are the midpoints of the sides of this quadrilateral." ... more
- "ABCDOE is a regular hexagon with O as origin. The position vector of A is \(a\) and the position vector of B is \(b\)." ... more
- "Consider a triangle ABC where M is the midpoint of AB and F is the point on BC where BF:FC = 3:4." ... more
- "In the parallelogram OABC two of the sides can be represented by vectors \(a\) and \(c\)." ... more
- "ABCD is a quadrilateral" ... more
- "(a) If A is the point (3,5) write down the position vector of A." ... more
- "In the diagram above (not drawn to scale) \(X\) is the point on \(AB\) such that \(AX:XB = 9:4\)." ... more
- "Consider two perpendicular vectors \(p\) and \(q\)." ... more
- "Two points \(A\) and \(B\) have coordinates (1 , 3 , 6) and (8 , 7 , 10) respectively." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Geometry Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of a formal mathematical science emerging in the West as early 6th Century BC. See also the topics of Angles, Area, Bearings, Circles, Enlargements, Mensuration, Pythagoras, Shape, Shape (3D), Symmetry, Transformations and Trigonometry.
- Vectors Vectors usually first make an appearance when pupils learn about transformations. A translation is best described with a vector written as a two by one matrix. Following that pupils learn how vectors can be used to prove geometric relationships in simple line diagrams. Ultimately vectors are studied as a major topic for A Level and International Baccalaureate courses where vectors in three dimensions are included.You can think of a vector as what is needed to 'carry' the point A to the point B. The Latin word vector means ‘carrier’ and was first used by 18th century astronomers investigating planet rotation around the Sun.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Lyric Lacking Limerick
Find the words missing from the mathematical limerick.
2nd Lesson
Product Placement
Arrange the numbers to produce the largest product.
3rd Lesson
Pyramid Puzzle
Arrange numbers at the bottom of the pyramid which will give the largest total at the top.
4th Lesson
Quad Areas
Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
5th Lesson
Roman Numerals
Learn a very different method for writing numbers using Roman numerals.
6th Lesson
Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
