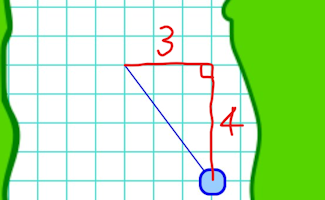
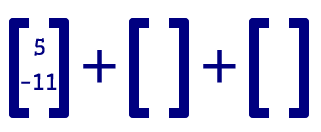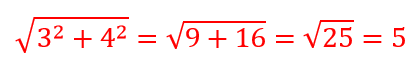|
|
||
Transum.orgThis web site contains over a thousand free mathematical activities for teachers and pupils. Click here to go to the main page which links to all of the resources available. Please contact me if you have any suggestions or questions.
|
More Activities: |
|
|
Mathematicians are not the people who find Maths easy; they are the people who enjoy how mystifying, puzzling and hard it is. Are you a mathematician? Comment recorded on the s /Indice 'Starter of the Day' page by Busolla, Australia: "Thank you very much for providing these resources for free for teachers and students. It has been engaging for the students - all trying to reach their highest level and competing with their peers while also learning. Thank you very much!" Comment recorded on the 26 March 'Starter of the Day' page by Julie Reakes, The English College, Dubai: "It's great to have a starter that's timed and focuses the attention of everyone fully. I told them in advance I would do 10 then record their percentages." |
Each month a newsletter is published containing details of the new additions to the Transum website and a new puzzle of the month. The newsletter is then duplicated as a podcast which is available on the major delivery networks. You can listen to the podcast while you are commuting, exercising or relaxing. Transum breaking news is available on Twitter @Transum and if that's not enough there is also a Transum Facebook page. |
|
Numeracy"Numeracy is a proficiency which is developed mainly in Mathematics but also in other subjects. It is more than an ability to do basic arithmetic. It involves developing confidence and competence with numbers and measures. It requires understanding of the number system, a repertoire of mathematical techniques, and an inclination and ability to solve quantitative or spatial problems in a range of contexts. Numeracy also demands understanding of the ways in which data are gathered by counting and measuring, and presented in graphs, diagrams, charts and tables." Secondary National Strategy, Mathematics at key stage 3 |
||
Go MathsLearning and understanding Mathematics, at every level, requires learner engagement. Mathematics is not a spectator sport. Sometimes traditional teaching fails to actively involve students. One way to address the problem is through the use of interactive activities and this web site provides many of those. The Go Maths main page links to more activities designed for students in upper Secondary/High school. | ||
Teachers | ||
|
If you found this activity useful don't forget to record it in your scheme of work or learning management system. The short URL, ready to be copied and pasted, is as follows: |
Alternatively, if you use Google Classroom, all you have to do is click on the green icon below in order to add this activity to one of your classes. |
It may be worth remembering that if Transum.org should go offline for whatever reason, there are mirror site at Transum.info that contains most of the resources that are available here on Transum.org. When planning to use technology in your lesson always have a plan B! |
|
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments. |
||