Integration
Term 1 starting in week 4 :: Estimated time: 1 weeks
- 5.5 Integration.
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
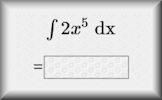 Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions.
Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions. Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.
Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.
Here are some exam-style questions on this topic:
- "The graph of \(f(x)=8-x^2\) crosses the x-axis at the points A and B." ... more
- "The acceleration, \(a\) ms-2 , of an object at time \(t\) seconds is given by" ... more
- "(a) Find \(\int (4x+5) dx\)." ... more
- "Given that \( \frac{dy}{dx} = \sin(x + \frac{\pi}{3})\) and \(y = 5\) when \(x = \frac{8\pi}{3}\), find \(y\) in terms of \(x\)." ... more
- "A particle moves in a straight line. During the first nine seconds the velocity, \(v\) ms-1 of the particle at time \(t\) seconds is given by:
$$ v(t) = t \cos(t+5) $$
The following diagram shows the graph of v:
" ... more - "The following diagram shows part of the graph of:" ... more
- "Consider the graph of the function \(f(x)=x^2+2\)." ... more
- "(a) Express the algebraic fraction" ... more
- "Make a sketch of a graph showing the velocity (in \(ms^{-1}\)) against time of a particle travelling for six seconds according to the equation:" ... more
- "Find the value of \(a\) if \(\pi \lt a \lt 2\pi\) and:" ... more
- "This graph represents the function \(f:x\to a \cos x, a\in \mathbf N\)" ... more
- "Find \(f(x)\) if \(f'(x)=6 \sin2x\) and the graph of \(f(x)\) passes through the point \((\frac{\pi}{3},11)\)." ... more
- "The diagram shows a sketch of the curve C with equation:" ... more
- "The following diagram shows the graph of \(f(x) = \cos(e^x) \; \text{for} \; 0 \le x \le 0.5\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.

