HCF and LCM

Instructions Try your best to answer the questions above. Type your answers into the boxes provided leaving no spaces. As you work through the exercise regularly click the "check" button. If you have any wrong answers, do your best to do corrections but if there is anything you don't understand, please ask your teacher for help. When you have got all of the questions correct you may want to print out this page and paste it into your exercise book. If you keep your work in an ePortfolio you could take a screen shot of your answers and paste that into your Maths file.

	You are learning this because future ideas are built on previous ideas and the more ideas you learn the more power you have to learn anything, ever! The world's best football player engages in rigorous training, practicing skills repeatedly to prepare for the big game. While the specific actions rehearsed during these exercises are rarely needed in the match, the very process of performing these drills enhances their overall prowess as a top player. more...	More Activities: Maths Map Go Maths Games Puzzles Times Tables TablesMaster iPad Maths Investigations Exam Questions
Mathematicians are not the people who find Maths easy; they are the people who enjoy how mystifying, puzzling and hard it is. Are you a mathematician? Comment recorded on the 19 November 'Starter of the Day' page by Lesley Sewell, Ysgol Aberconwy, Wales: "A Maths colleague introduced me to your web site and I love to use it. The questions are so varied I can use them with all of my classes, I even let year 13 have a go at some of them. I like being able to access Starters for the whole month so I can use favourites with classes I see at different times of the week. Thanks." Comment recorded on the 8 May 'Starter of the Day' page by Mr Smith, West Sussex, UK: "I am an NQT and have only just discovered this website. I nearly wet my pants with joy. To the creator of this website and all of those teachers who have contributed to it, I would like to say a big THANK YOU!!! :)."		Each month a newsletter is published containing details of the new additions to the Transum website and a new puzzle of the month. The newsletter is then duplicated as a podcast which is available on the major delivery networks. You can listen to the podcast while you are commuting, exercising or relaxing. Transum breaking news is available on Twitter @Transum and if that's not enough there is also a Transum Facebook page.
Featured Activity Online Logo An opportunity for students to write a computer program. There is nothing to download, all of the interaction takes place in the browser. Great for understanding angles and the properties of shapes.	Answers There are answers to this exercise but they are available in this space to teachers, tutors and parents who have logged in to their Transum subscription on this computer. A Transum subscription unlocks the answers to the online exercises, quizzes and puzzles. It also provides the teacher with access to quality external links on each of the Transum Topic pages and the facility to add to the collection themselves. Subscribers can manage class lists, lesson plans and assessment data in the Class Admin application and have access to reports of the Transum Trophies earned by class members. If you would like to enjoy ad-free access to the thousands of Transum resources, receive our monthly newsletter, unlock the printable worksheets and see our Maths Lesson Finishers then sign up for a subscription now: Subscribe
Go Maths Learning and understanding Mathematics, at every level, requires learner engagement. Mathematics is not a spectator sport. Sometimes traditional teaching fails to actively involve students. One way to address the problem is through the use of interactive activities and this web site provides many of those. The Go Maths page is an alphabetical list of free activities designed for students in Secondary/High school. Maths Map Are you looking for something specific? An exercise to supplement the topic you are studying at school at the moment perhaps. Navigate using our Maths Map to find exercises, puzzles and Maths lesson starters grouped by topic.
Teachers
If you found this activity useful don't forget to record it in your scheme of work or learning management system. The short URL, ready to be copied and pasted, is as follows:	Alternatively, if you use Google Classroom, all you have to do is click on the green icon below in order to add this activity to one of your classes.	It may be worth remembering that if Transum.org should go offline for whatever reason, there is a mirror site at Transum.info that contains most of the resources that are available here on Transum.org. When planning to use technology in your lesson always have a plan B!
Transum, Monday, May 13, 2024 "In my student days I worked my summers in America; at Camp Tamarack in New Jersey. I remember in 1979 being surrounded by large colourful insects called cicadas which can only be seen every 17 years. In 2024, Illinois is experiencing a rare natural spectacle: the simultaneous emergence of cicada Broods XIII and XIX. This event, first recorded in 1803, won’t occur again until 2245. These periodical cicadas, which emerge either every 13 or 17 years, spend the majority of their lives underground, only surfacing to reproduce at the end of their long developmental cycles. After mating, females lay approximately 500 to 600 eggs in woody plants before the adults die, their life above ground lasting merely a month. The eggs hatch six weeks later, and the nymphs burrow into the soil to begin their 13 or 17-year cycle. This synchronisation of 13 and 17-year cycles is a perfect natural example of common multiples. " Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.

For Students:

For Teachers:

For All:

Transum.org is a proud supporter of the kidSAFE Seal Program

Description of Levels

Sieve Use the Sieve of Eratosthenes to find prime numbers.

Factor Trees An interactive and very visual way to break down a number into its prime factors.

Level 1 - Finding the highest common factor (HCF) of two numbers.

Level 2 - Finding the lowest common multiple (LCM) of two numbers

Level 3 - Finding the highest common factor (HCF) of large numbers.

Level 4 - Finding the lowest common multiple (LCM) of large numbers

Level 5 - Finding the HCF and LCM of three numbers

Level 6 - Given the HCF and LCM find the numbers

Level 7 - Mixed application questions

HCF and LCM given An Advanced Lesson Starter.

Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.

Curriculum Reference

See the National Curriculum page for links to related online activities and resources.

Help

The highest common factor (HCF) of two numbers is the largest number that divides exactly into both of the numbers.

You can Find the HCF of numbers by listing the prime factors of both numbers then multiplying together the factors that appear in both lists.

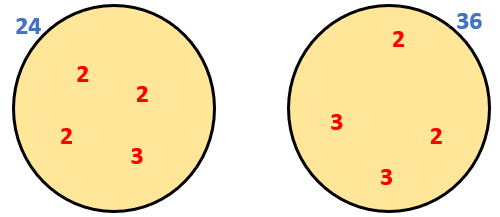
For example find the HCF of 24 and 36
24 = 2x2x2x3 and 36 = 2x2x3x3
so the HCF of 24 and 36 is 2x2x3 = 12

The lowest common multiple (LCM), or least common multiple, is the smallest number that both numbers divide into exactly.

You can Find the LCM of numbers by listing the prime factors of both numbers and then multiply all the prime factors of the larger number by those prime factors of the smaller number that are not already included.

For example find the LCM of 24 and 36
24 = 2x2x2x3 and 36 = 2x2x3x3
so the LCM of 24 and 36 is 2x2x3x3 x 2 = 72

Venn Diagram

A Venn diagram may help you with the task of finding the HCF and LCM of 24 and 36.

Express each number as the primes which multiplied together would give you that number. Write them in Venn diagram sets:

Show the sets intersecting

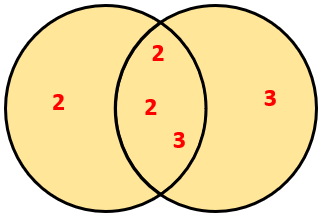
Multiply the numbers in the intersection of the sets to find the HCF, 2x2x3 = 12.

Multiply all the numbers in the overlapping sets diagram to find the LCM, 2x2x2x3x3 = 72.

The Indian Method

Click here to see an animated demonstration of this cool way to find both the HCF and LCM of two numbers.

A Calculator Method

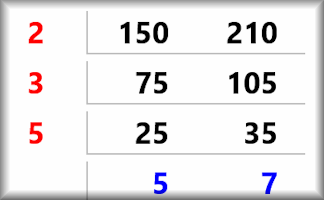
Advanced calculators have built in functions for finding the HCF and LCM of two numbers but there is a trick for finding the HCF using a modern scientific calculator.

If the two numbers are entered using the fraction template the calculator will express that fraction in its lowest terms. It does this by dividing numerator and denominator by their HCF.

For example to find the HCF of 24 and 36 enter 24/36 then press enter.

Considering the denominators, we now need to find what 24 was divided by to give 2. So dividing 24 by 2 gives 12 which is the HCF.

Connecting HCF and LCM

When you have found the HCF of the numbers a and b the LCM can be found using the following formula:

LCM = ab ÷ HCF

Greatest Common Divisor

It is worth knowing that HCF is also known as GCD. If you are using a spreadsheet such as Excel there are functions named LCM and GCD for calculating the LCM and HCF.

Don't wait until you have finished the exercise before you click on the 'Check' button. Click it often as you work through the questions to see if you are answering them correctly.

1. Mr Bytheway was celebrating his birthday. He noticed that his age was divisible by 7 and 13. How old was Mr Bytheway?
2. Len has been baking cakes for the school Fun Day Fete. He has made 141 Iced buns and 235 chocolate chip muffins. He wants to create some identical refreshment tables that will operate during the day. Each table will have the same number of each type of cake. What is the greatest number of refreshment tables that Len can stock?	tables
3. The 17-year locust (Magicicada) can only be seen every 17 years. The 13-year locust only appears every 13 years. If they were both seen in the year 2020, in which year would they next both appear together?
4. Playtime Playground Equipment Ltd. would like to donate 210 swings and 60 roundabouts to parks around the country. The company would like to make sure that each park receives the same number of swings and roundabouts with none left over. What is the greatest number of parks that the company can donate to?	parks
5. Every 84 seconds I hear a ding Every 56 seconds I hear a dong I started a timer when I heard dong-ding To hear it again I must wait how long?	seconds
6. Noreen and Doreen were flower arrangers. Noreen included 33 flowers in each of her arrangements while Doreen included 44 flowers in each of hers. At the end of a month they realised that they had both used the same total number of flowers in the arrangements they had made. What is the smallest that total could have been?	flowers
7. At a District Scout Camp the Scouts could form teams of 7, 14 or 20 with no Scout left out. What was the least number of Scouts that could have been at the camp?	Scouts
8. Three pieces of string have lengths 124cm, 286cm and 320cm. They are each to be cut into pieces of the same length so that no string is left over. What is the longest this length could be?	cm
9. Tess O'late has a rectangular canvas measuring 240cm by 150cm. She wants to fill the canvas with painted tessellating squares. What is the smallest number of squares she must paint to fill the canvas?	squares
10. There are stepping stones across Silver Stream. The stones are numbered from one to fifty three. The green frog starts on stone number one and crosses the stream by jumping to every other stone. The brown frog starts on stone number one but jumps over two stones to land on the next as it crosses the stream. The mighty teal frog starts on stone number one but jumps over six stones to land on the next as it crosses the stream. Which stone (other than stone number one) will all three frogs visit?
11. Nora, Dora and Jora are three friends who do not know much about healthy eating. Nora had £7.74 Dora had £9.58 Jora had £6.59 Nora, Dora and Jora each bought as many gobstoppers as they could with their money. They realised that they each then had exactly 15p left over. What is the greatest possible cost of a gobstopper?	p
12. What is the smallest whole number that is exactly divisible by two thirds, four fifths and one half?

HCF and LCM

Practise finding the highest common factor (HCF), sometimes called the greatest common divisor, and the lowest common multiple (LCM) of two numbers.

Menu Trees Level 1 Level 2 Level 3 Level 4 Level 5 Level 6 Level 7 Help More

Instructions

More Activities:

Featured Activity

Online Logo

Answers

Go Maths

Maths Map

Teachers