Answer
Sign in to your Transum subscription account to see the answers
Note to teacher: Doing this activity once with a class helps students develop strategies. It is only when they do this activity a second time that they will have the opportunity to practise those strategies. That is when the learning is consolidated. Click the button above to regenerate another version of this starter from random numbers.
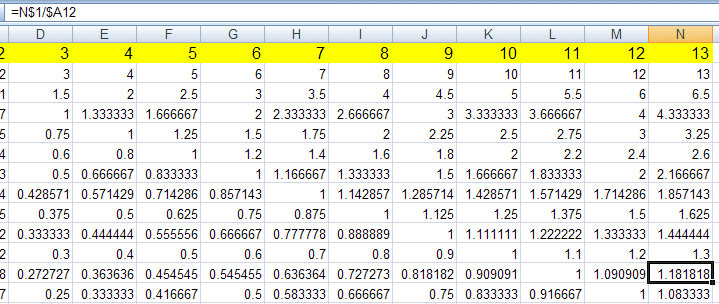
A spreadsheet could be used to quickly find a solution to this kind of problem.
Your access to the majority of the Transum resources continues to be free but you can help support the continued growth of the website by doing your Amazon shopping using the links on this page. Below is an Amazon link. As an Amazon Associate I earn a small amount from qualifying purchases which helps pay for the upkeep of this website.
Educational Technology on Amazon
|
Change the background of this page to
or
for clearer classroom display.
|
||

|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=July6 However it would be better to assign one of the student interactive activities below. |
|
Use a spreadsheet to help investigate which pairs of numbers, when divided, give a recurring decimal answer.
Here is the URL which will take them to a student version of this activity.



